他の年度については、コチラからどうぞ。
サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
解説の内容自体に影響はありません。
問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。
5
(1) $~4\cos^3{x}-3\cos{x}~$
(2) $~\displaystyle 0,\frac{\pi}{2},\pi,\frac{3}{2}\pi,2\pi~$
(3) $~\displaystyle \frac{16}{3}$
5(1)
加法定理や2倍角の公式を使って式変形していくと、
\begin{align}
&\cos{3x} \\
&=\cos{(x+2x)} \\
&=\cos{x}\cos{2x}-\sin{x}\sin{2x} \\
&=\cos{x}(2\cos^2{x}-1)-\sin{x}(2\sin{x}\cos{x}) \\
&=2\cos^3{x}-\cos{x}-2\cos{x}\sin^2{x} \\
&=2\cos^3{x}-\cos{x}-2\cos{x}(1-\cos^2{x}) \\
&=2\cos^3{x}-\cos{x}-2\cos{x}+2\cos^3{x} \\
&=4\cos^3{x}-3\cos{x}
\end{align}
\begin{align}
&\cos{3x} \\
&=\cos{(x+2x)} \\
&=\cos{x}\cos{2x}-\sin{x}\sin{2x} \\
&=\cos{x}(2\cos^2{x}-1) \\
&-\sin{x}(2\sin{x}\cos{x}) \\
\\
&=2\cos^3{x}-\cos{x}-2\cos{x}\sin^2{x} \\
&=2\cos^3{x}-\cos{x}-2\cos{x}(1-\cos^2{x}) \\
&=2\cos^3{x}-\cos{x}-2\cos{x}+2\cos^3{x} \\
&=4\cos^3{x}-3\cos{x}
\end{align}
が求まった。
5(2)
$~C_{2}~$ の $~y~$ を $~C_{1}~$ の $~y~$ に代入すると、
\begin{equation}
\cos{3x} =\displaystyle \sin{ \left( x+\frac{\pi}{2} \right)}
\end{equation}
であり、 $~\displaystyle \sin{ \left( x+\frac{\pi}{2} \right)} =\cos{x}~$ であることを使って、式変形していくと、
\begin{align}
\cos{3x}&=\cos{x} \\
\cos{3x}-\cos{x}&=0 \\
4\cos^3{x}-3\cos{x}-\cos{x}&=0 \\
4\cos^3{x}-4\cos{x}&=0 \\
4\cos{x}(\cos^2{x}-1)&=0 \\
4\cos{x}(\cos{x}+1)(\cos{x}-1)&=0 \\
\end{align}
であり、
\begin{equation}
\cos{x}=-1,0,1
\end{equation}
が求まる。
$~0 \le x \le 2\pi~$ の範囲で、それぞれの $~x~$ の値を考えると、
\begin{align}
& \displaystyle \cos{x}=-1 より、x=\pi \\
\\
& \cos{x}=0 より、x=\frac{\pi}{2},\frac{3}{2}\pi \\
\\
& \cos{x}=1 より、x=0,2\pi \\
\end{align}
である。まとめて、
\begin{equation}
\displaystyle 0,\frac{\pi}{2},\pi,\frac{3}{2}\pi,2\pi
\end{equation}
が求まった。
5(3)
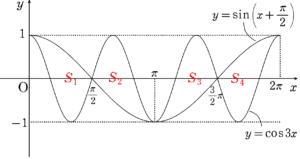
$~C_{1},C_{2}~$ をそれぞれグラフにすると、次のようになる。
上図で示した $~S_{1},S_{2},S_{3},S_{4}~$ は、すべて対称的な図形であるため、面積は等しい。
したがって、 $~S_{1}~$ を求めると、
\begin{align}
\displaystyle S_{1}&=\int_{0}^{\frac{\pi}{2}} \sin{ \left( x+\frac{\pi}{2} \right)}-\cos{3x}dx \\
\\
&=\int_{0}^{\frac{\pi}{2}} \cos{x}-\cos{3x}dx \\
\\
&=\left[ \sin{x}-\frac{1}{3}\sin{3x} \right]_{0}^{\frac{\pi}{2}} \\
\\
&=1-\frac{1}{3}\cdot (-1) \\
\\
&=\frac{4}{3}
\end{align}
であるため、これを $~4~$ 倍することで、 $~\displaystyle \frac{16}{3}~$ が求まった。
なぜ $~C_{1}~$ が、 $~\displaystyle y=\sin{ \left( x+\frac{\pi}{2} \right)}~$ と表記されていたのかが謎・・・。 $~\cos{x}~$ であることに気付けないと、ハマリそうです・・・。

◇参考文献等
・『私学教員適性検査問題集 数学(平成29年度~31年度)』
コメント