【数学史３－７】ピタゴラスの定理はバビロニアが最初？粘土板の表に隠された秘密とは？

　直角三角形の辺の長さの関係を表す「三平方の定理」。
　別名「ピタゴラスの定理」とも呼ばれるため、古代ギリシャの数学者ピタゴラスが発見したと考えられがちです。

　しかし、実際はピタゴラスが生まれる1000年以上前から、バビロニアに存在し、研究されていたことがわかっています。

　この記事では、バビロニアで三平方の定理が使われていた根拠となる粘土板について解説。

　現在の数学では見られない、ピタゴラス数の表について知ることができます。

ピタゴラス数が記されている粘土板

　紀元前1800年頃に書かれたとされる粘土板プリンプトン322には、バビロニア人が三平方の定理を知っていたとわかる数表が残っていました。

　この粘土板に載っていたピタゴラス数について、見てみましょう。

ピタゴラス数は三平方の定理を満たす整数組

　そもそも「ピタゴラス数」とは、ピタゴラスの定理を満たす整数の組を指します。

　ピタゴラスの定理は別名「三平方の定理」とも言い、中学3年生で学ぶ以下のような定理です。

ピタゴラスの定理

　直角をはさむ辺の長さが$~a~,~b~$、斜辺が$~c~$である直角三角形において、

a^2+b^2=c^2

が成り立つ。

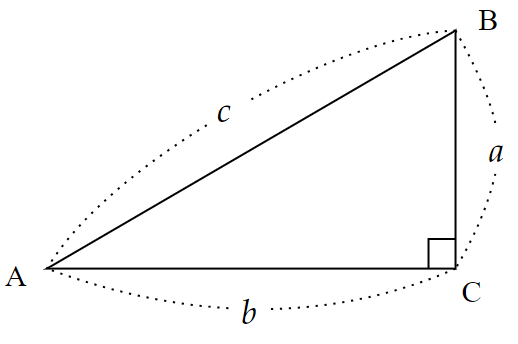
　この定理を満たす整数の組は、以下のようなものが挙げられます。

• $~a=3~,~b=4~,~c=5~$
• $~a=5~,~b=12~,~c=13~$
• $~a=7~,~b=24~,~c=25~$

　それぞれの組の自然数倍もピタゴラス数となるため、無限に存在します。

プリンプトン322には15組のピタゴラス数が記載

　紀元前1800年頃に書かれたとされる、粘土板プリンプトン322には、バビロニアお得意の数表の中でも、ピタゴラス数をリスト化したものが記載されていました。

　まずはこれをバビロニアの数字のまま書き出すと、下の＜表3＞のようになります。（「;」は小数点、「,」は位の境目を表す。）

　これを今の数字に直し、直角三角形の3辺$~a~,~b~,~c~$のどの値かを明らかにしたうえで、列を1つ補足して書くと、下の＜表4＞のようになります。

　$~a~$の値については、$~\displaystyle \left( \frac{c}{a} \right)^2~$の値から算出しています。

　一見、ピタゴラス数が不規則に並んでいるように見えますが、ある規則に従って（後述）並べられているのです。

ピタゴラス数の見つけ方

　表4の数値はどのようにして求められたのでしょうか。

　きちんとした理論に基づいて、ピタゴラス数が求められていたことがわかっています。

バビロニアでは逆数表から求めた

　二次方程式$~x^2-px+q=0~$を解く鍵にもなっていた恒等式と、逆数表を合わせることでピタゴラス数をたくさん見つけることが可能でした。

ピタゴラス数の導き方

　バビロニアでよく使われていた以下の恒等式を利用する。

xy+\left( \frac{x-y}{2} \right)^2=\left( \frac{x+y}{2} \right)^2~~~\cdots①

　＜図5＞のような、３辺が$~a’=xy=1~$、$~b’=\displaystyle \frac{x-y}{2}~$、$~c’=\displaystyle \frac{x+y}{2}~$の直角三角形を考える。

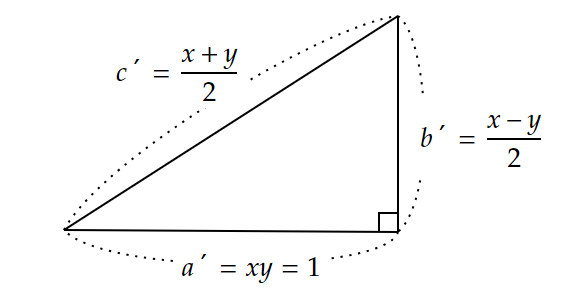
　このとき、$①$から、

(a')^2+(b')^2=(c')^2~~~~\cdots②

となり、$~xy=1~$を満たす$~x~,~y~$の組を求めればよいことがわかる。

　$~x~$と$~y~$は逆数の関係にあるため、逆数表から逆数の関係にある２つの数を選べば、$②$を満たす$~a’~,~b’~,~c’~$は求まる。

　１辺の長さを$~a^{\prime}=xy=1~$と固定してあげることで、バビロニアお得意の数表にもっていく導き方でした。

ピタゴラス数(119,120,169)を求めてみた

　実際に逆数を使って、ピタゴラス数を１組求めてみましょう。

\begin{align*}
b'&=\frac{x-y}{2} \\
\\
&=\frac{\frac{12}{5}-\frac{5}{12}}{2} \\
\\
&=\frac{144-25}{120} \\
\\
&=\frac{119}{120}　\\
\\
c'&=\frac{x+y}{2} \\
\\
&=\frac{\frac{12}{5}+\frac{5}{12}}{2} \\
\\
&=\frac{144+25}{120} \\
\\
&=\frac{169}{120}
\end{align*}

1^2+\left( \frac{119}{120} \right)^2=\left( \frac{169}{120} \right)^2~~~~\cdots③

　バビロニアの書記による記述はここで終わっています。

　$③$により、$~b=119~,~c=169~,~\displaystyle \left(\frac{c}{a}\right)^2=\left(\frac{169}{120}\right)^2=1.9834028~$がわかり、それらの値はプリンプトン322の表に載っています。

　ちなみにですが、今の我々にとっては、$③$の両辺を$~120^2~$倍して、

120^2+119^2=169^2

としたほうが、理解しやすいです。

三平方の定理がバビロニアで知られていた根拠

　ここまでの話だと、$~a^2+b^2=c^2~$を満たす自然数の組を求める方法が知られていたことはわかるものの、この$~a~,~b~,~c~$が直角三角形の三辺に対応することまで知られていたかは断言できません。

しかし、粘土板プリンプトン322（表4）の$~\displaystyle \left( \frac{c}{a} \right)^2~$の値に注目すると、明らかに直角三角形を意識していたことがわかります。

tanθと数表の関係

　図7の直角三角形の角度$~\theta~$について考えてみましょう。

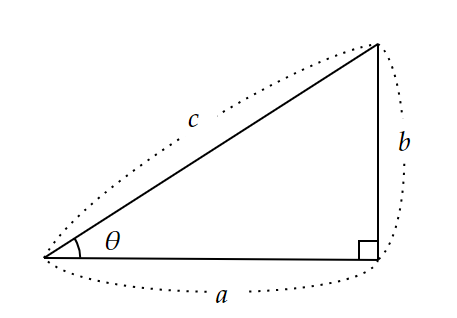
　$~\tan{\theta}=\displaystyle \frac{b}{a}~$を三角比の相互関係を使って、式変形すると

\begin{align*}
\tan^2{\theta}&=\frac{1}{\cos^2{\theta}}-1 \\
\\
&=\frac{1}{\left(\frac{a}{c}\right)^2}-1 \\
\\
&=\left(\frac{c}{a}\right)^2-1 \\
\end{align*}

であり、表4の$~\displaystyle \left(\frac{c}{a}\right)^2~$と$~\theta~$のつながりが見えてきます。

数表の順番は角度で決まっていた

　実は、表4のピタゴラス数の順番は、角度$~\theta~$の大きい順になっているのです。

　表4にある$~\displaystyle \left(\frac{c}{a}\right)^2~$の値から$~1~$をひくことで、$~\tan^2{\theta}~$が求まり、さらには$~\tan{\theta}~$や$~\theta~$の値を考えてあげると、以下の表8のようになります。

　角度$~\theta~$はほぼ等差数列のように減少しています。
 
　この事実から、バビロニア人は角度$~\theta~$を考えていた、すなわち直角三角形における$~a^2+b^2=c^2~$を知っていたということがわかるのです。

まとめ・参考文献

　バビロニアにおける三平方の定理を、ピタゴラス数の表をもとに解説してきました。　

• 粘土版プリンプトン322にはピタゴラス数が15組載っていた
• その数表は、角度の大きい順に並んでいる。
• ピタゴラス数の求め方は、恒等式と逆数表の応用。

　一見すると、無作為にピタゴラス数が並んでいるように見えて、実は角度の大きい順というのが素敵ですね。

　次の記事では、バビロニアにおける平方根の値の求め方について解説します。

次の記事へ

【数学史３－８】バビロニアでは平方根の研究も？粘土板に残された√2の値とは？ 三平方の定理や二次方程式を扱っていたバビロニア。当然必要となるのは平方根の知識であり、バビロニアの粘土板YBC7289から、√2の近似値が1.41421296 と求まっていたことがわかっています。ここまで緻密な値を求めるにあたって、利用されたのは相加相乗平均の考え方。その驚きの求め方をこの記事では解説します。

この章のまとめへ

【数学史まとめ３】バビロニアの数学 　メソポタミアの数学のことを、数学史上では「バビロニアの数学」と言い表します。紀元前1750年頃に数体系が確立していたバビロニア。実生活で使う範囲を超えた数学の記録が粘土板に今も残っています。この記事では、バビロニアの数学に関する事柄を年表形式でまとめると共に、バビロニアが紀元前に誇った高度な数学を大まかに解説します。

なんでもかんでも数表。バビロニア人の活用力がすごい！

角度が等差数列的に並ぶのが神秘的。見つかってはいないようだけど、三角比の数表もあったんだろうね。