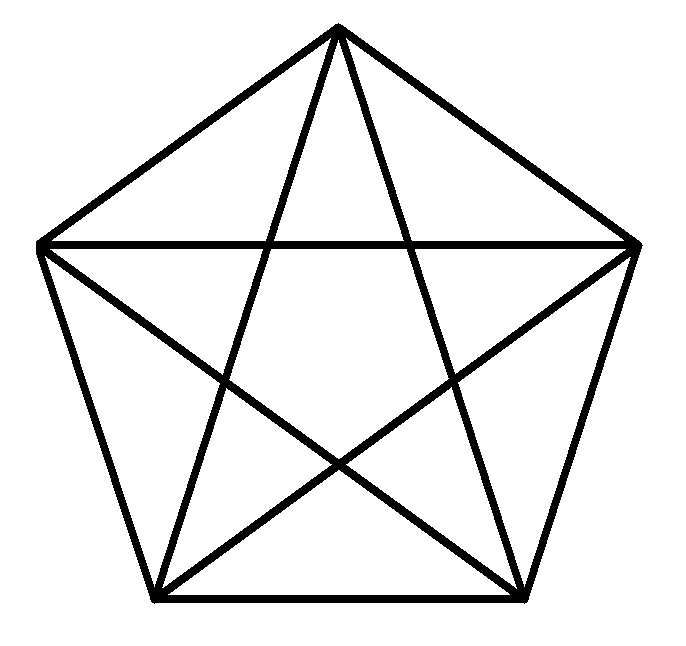
1つの内角の大きさが$~72^{\circ}~$、1辺の長さと対角線の長さの比が$~\displaystyle 1:\frac{1+\sqrt{5}}{2}~$(黄金比)である正五角形。
実は、正五角形は定規とコンパスだけで書くことができ、その方法は紀元前から知られていました。
この記事では、正五角形の作図方法と、それによってなぜ正確な作図ができるのかを証明!
作図の手順こそ多いものの、1ステップずつ図を使って解説します。
正五角形の作図方法
正五角形は、1つの内角が$~108^{\circ}~$という中途半端な角であり、一辺と対角線の長さの比に無理数である黄金比$~\left( \displaystyle 1:\frac{1+\sqrt{5}}{2} \right)~$が出てくる図形であることから、作図は難しそうに思えます。
しかし、正五角形はコンパスと定規だけで作図ができ、その作図の歴史は紀元前にまでさかのぼるのです。
ピタゴラスが初めて作図をした
正五角形の作図を世界で初めて行ったとされるのが、古代ギリシャの数学者ピタゴラス(Pythagoras , B.C.569頃~B.C.500頃)。

(出典:The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons)
ピタゴラスは、自身が作った宗教団体「ピタゴラス教団」のシンボルマークに正五角形を採用し、その作図ができたことを誇示していました。
ピタゴラスが行った正五角形の作図方法は定かではありませんが、三平方の定理の証明を初めて行った彼だからこそ、正五角形の作図もできたのでしょう。

5ステップで作図ができる
ピタゴラスの時代に知られていた知識だけで、正五角形の作図は可能です。
必要な手数は5ステップ。
黄金比である$~\displaystyle 1:\frac{1+\sqrt{5}}{2}~$をうまく利用します。
与えられた線分$~AB~$を一辺とする正五角形を作図する。
与えられた線分$~AB~$の垂直二等分線$~\ell~$をかく。

$~AB~$と$~\ell~$の交点を$~L~$とする。
$~AB~$の長さをコンパスでとり、$~L~$からの距離が$~AB~$と同じになる点$~M~$を$~\ell~$上にとる。

ちなみに、$~M~$は$~AB~$の上側と下側のどちらでもよい。(図4は上側)
$~B~$を中心とし、半径$~BM~$の円と半直線$~AB~$の交点$~N~$をとる。

$~LN~$の長さをコンパスでとり、 $~A~$を中心とした半径$~LN~$の円$~P~$と、$~B~$を中心とした半径$~LN~$の円$~Q~$をかく。

このとき、円$~P~$と円$~Q~$の交点が、正五角形$~ABCDE~$の頂点$~D~$となる。
$~AB~$の長さをコンパスでとり、 $~B~$を中心とした半径$~AB~$の円$~R~$と、$~A~$を中心とした半径$~AB~$の円$~s~$をかく。

このとき、円$~P~$と円$~R~$の交点が、正五角形$~ABCDE~$の頂点$~C~$となり、円$~Q~$と円$~S~$の交点が、正五角形$~ABCDE~$の頂点$~E~$となるため、$~A,B,C,D,E~$を結べば正五角形が完成する。
正三角形や正四角形、正六角形と比べて作図方法が複雑ですが、以上の5ステップで正五角形をきれいに作図することができます。
作図できる理由
なぜ ★正五角形の作図方法 で作図ができるのでしょうか?
その理由を、各線分の長さを計算することによって証明していきます。
辺と対角線の関係が鍵
証明の前提知識として、正五角形の辺と対角線の関係についておさらいしておきましょう。
正五角形の辺と対角線の比は、$~1~:~\phi~$となる。
ただし、$~\phi=\displaystyle \frac{1+\sqrt{5}}{2}~$で、$~\phi~$を黄金数という。
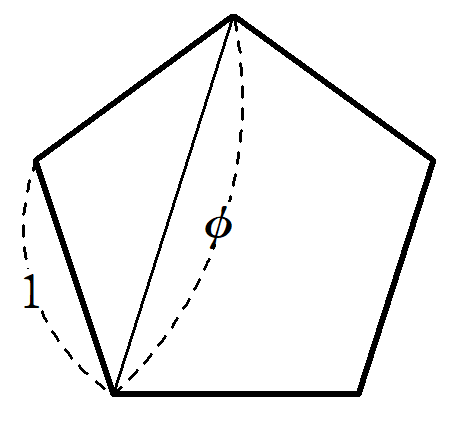
証明については、「正五角形と黄金比 」で解説しています。

線分$~AB~$を$~1~$としたとき、 $~\phi=\displaystyle \frac{1+\sqrt{5}}{2}~$の作図さえできれば、残りの頂点$~C~,~D~,~E~$を以下の図9の関係から求めることができます。
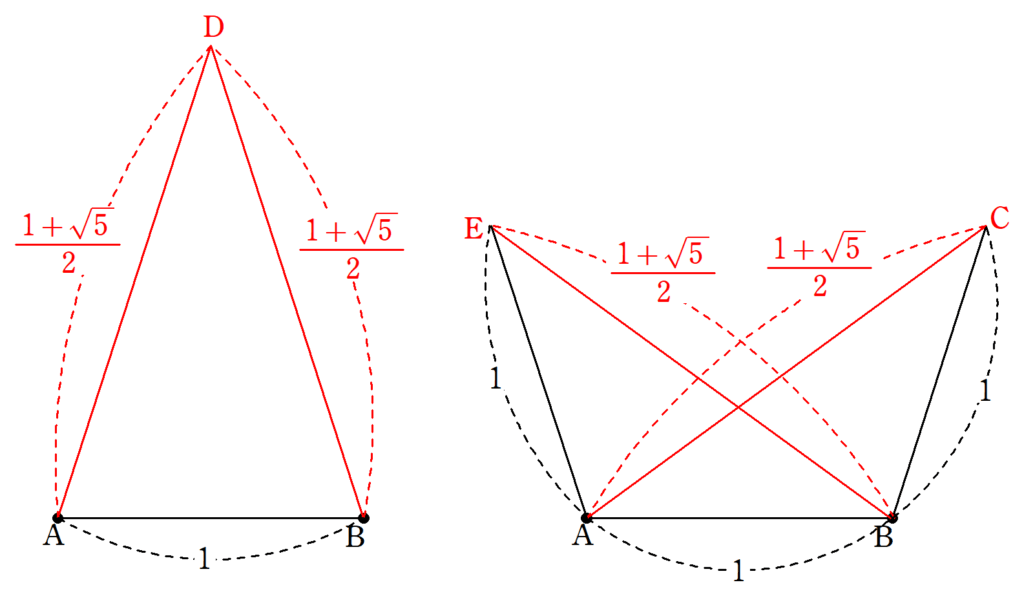
三平方の定理で黄金比を作図できる
では、 $~\phi=\displaystyle \frac{\sqrt{5}+1}{2}~$ がどのように作図されるのかという点に着目しながら、先ほどの作図方法を分析してみましょう。
与えられた線分$~AB=1~$を一辺とする正五角形を作図する。
垂直二等分線により、$~L~$は$~AB~$の中点なので、$~AL=BL=\displaystyle \frac{1}{2}~$となる。

$~AB=1~$であるため、$~LM=1~$となる。

半径となる$~BM~$の長さは、三平方の定理より、
\begin{align*}
BM&=\sqrt{\left(\frac{1}{2}\right)^2+1^2} \\
\\
&=\sqrt{\frac{5}{4}} \\
\\
&=\frac{\sqrt{5}}{2}
\end{align*}なので、$~BN=\displaystyle \frac{\sqrt{5}}{2}~$となる。

よって、
LN=\frac{1}{2}+\frac{\sqrt{5}}{2}=\frac{1+\sqrt{5}}{2}であり、黄金数を長さに持つ線分$~LN~$が作られた。
$~A~,~B~$を中心として、半径の長さが$~LN= \displaystyle \frac{1+\sqrt{5}}{2}~$の円$~P~,~Q~$をかいているため、それらの交点$~D~$は、$~AD=BD= \displaystyle \frac{1+\sqrt{5}}{2}~$を満たす。

$~A~,~B~$を中心として、半径の長さが$~AB=1~$の円$~R~,~S~$を書いているため、
- 円$~P~$と円$~R~$の交点$~C~$は、$~AC= \displaystyle \frac{1+\sqrt{5}}{2}~,~BC=1~$を満たす。
- 円$~Q~$と円$~S~$の交点$~E~$は、$~BE= \displaystyle \frac{1+\sqrt{5}}{2}~,~AE=1~$を満たす。

よって、$~A~,~B~,~C~,~D~,~E~$を結ぶことで、対角線の長さが黄金数である正五角形を作図することができる。
黄金数である$~\displaystyle \frac{1+\sqrt{5}}{2}~$を、$~\displaystyle \frac{1}{2} +\frac{\sqrt{5}}{2}~$と分けて考えることで、三平方の定理を活用して一辺が$~1~$の正五角形を作図することができました。
若い頃にバビロニアで三平方の定理を学び、ギリシャに帰ってからその証明まで行ったピタゴラスは、これと似たような方法で正五角形を作図したと考えられます。
まとめ
正五角形の作図の方法について解説してきました。
- 正五角形は定規とコンパスだけで作図ができる。
- 作図の方法では、三平方の定理が活用されている。
- 世界で最初に正五角形の作図をしたのはピタゴラス。
中3レベルの数学で理解できる作図方法なので、定規とコンパスを使って是非かいてみてください。
ピタゴラスの人生については、こちらで解説しています↓↓


こういう複雑なことまで考えてあげれば、どんな正多角形も作図できそうな気がするにゃ。



いや、正七角形や正九角形は作図不可能であることが証明されているんだ。
◇参考文献等
・三浦伸夫・三宅克哉監訳,久村典子訳(2018)『メルツバッハ&ボイヤー 数学の歴史Ⅰー数学の萌芽から17世紀前期までー』,pp.47-48,朝倉書店.

コメント
コメント一覧 (6件)
ひとつの内角は108°で、内角の和は520°になるかと
パッと見で1つの内角が直角を超えてますよね
ちなみに72°は、外角の360°を5等分するとこの値になります。
今のご時世ですから、この辺り入念に計算して表記しないとどんな言及がされてしまうのか……。
インターネット通信の構築を生業にしていた身としても、もはや想像が付かないので。
努努お気をつけください。
たゆたうさん
コメントありがとうございます。
正五角形の内角の表記を修正いたしました。
ご指摘いただき、ありがとうございます。
先に申し上げた事をご承知の上で作図されたのであれば、誠に失礼いたしました。
上のコンパスの使用法が許されるのならば、ユークリッド原論、第一巻命題2の作図法は無意味になりはしないでしょうか?
小林昭七先生の、円の数学、という書物の中に、コンパスを紙から離したら必ず折りたたむ、コンパスの脚を開いたまま別の場所へ持っていってはならない、と記されています。コンパスを長さのマーキングに使用してはいけないという意味だと思います。これに照らし合わせると上の作図法は間違っていないでしょうか?
岸川様
コメントいただきありがとうございます。
作図の定義に関しては、数学Aの教科書に準じて行いました。
❝定規とコンパスだけを用いて、与えられた条件を満たす図形をかくことを作図という❞
マーキングの使用の可否までは特に考えておりませんでした。
あくまで高校数学で定義された作図における、正五角形のかきかたとご理解いただければと思います。