四大文明から少し遅れて文明が発達した古代ギリシャ。
その特徴とも言えるポリス(国家)では、法によって統治され、その独特の風土から数学における証明の概念が生まれました。
この記事では、古代ギリシャの中でも、ギリシャ時代(~B.C.323)における世界史と数学の方向性、登場する数学者について解説。
現在では当たり前とされる数学の証明という概念を作った、ギリシャ時代の数学者たちの功績を知ることができます。
| 時代 | 紀元前2000年頃~紀元前323(アレクサンドロス大王の時代まで) |
| 場所 | ギリシャ |
古代ギリシャの歴史(ギリシャ時代まで)
古代ギリシャが世界史に登場するのは、紀元前2000年頃。
四大文明と比べると、少し遅めの幕開けでした。
文明の発生直後は争いが続いた
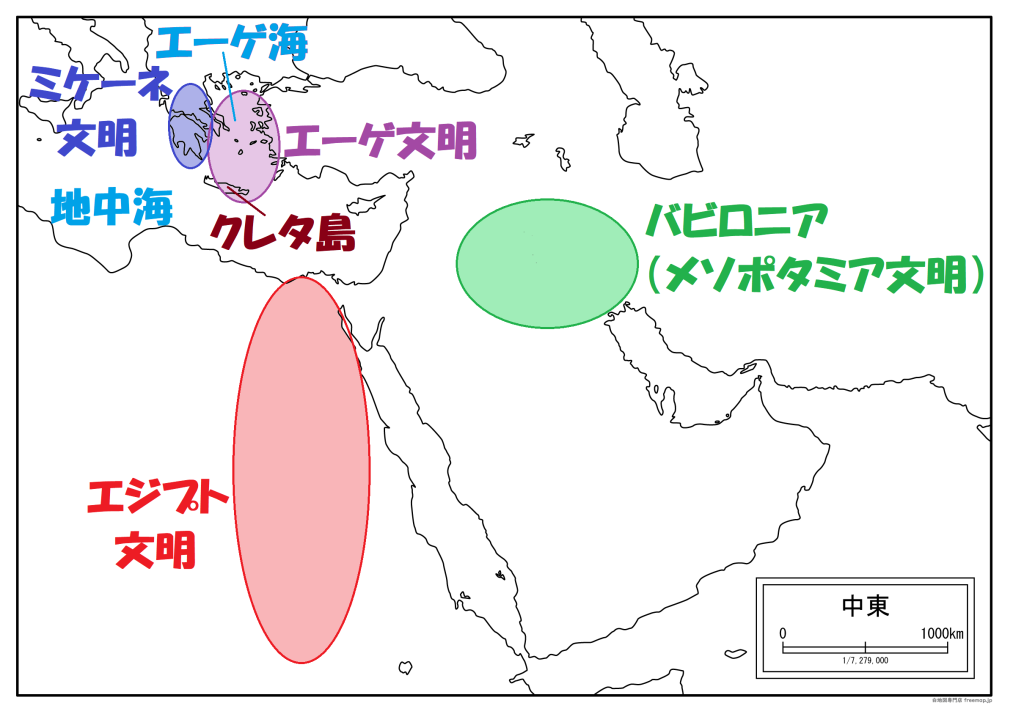
紀元前2000年頃から、エーゲ海に浮かぶクレタ島を中心に小さな国々が生まれ、エーゲ文明が誕生しました。
ギリシャ本土では、紀元前1600年頃にミケーネ文明が誕生。
好戦的なミケーネ文明は、紀元前15世紀にクレタ島を支配しました。
(出典:出典:白地図専門店より改変 / CC-BY-4.0)
ギリシャ本土を中心に、エーゲ海一帯で栄えたミケーネ文明は、紀元前1200年頃に破壊※1され、滅亡しました。
※1 破壊された理由は不明。気候変動や外部勢力の侵入などの様々な原因によるとされています。
その後の約400年間は、暗黒時代と呼ばれる混乱の時代となり、人々はギリシャ本土からエーゲ海の島々を中心に移住するようになります。
法で統治するポリスの誕生
紀元前8世紀に入ると、有力貴族を中心となって各地で人々が集住し、ポリスという都市国家ができ始めます。
ポリスの誕生が人々の定住をうながしたことで、約400年間続いた暗黒時代が終わりました。
紀元前7世紀頃になると、法律が成文化されるようになり、ポリス内は法で統治されるようになりました。

紀元前6世紀初頭には貴族だけでなく平民にも参政権が徐々に認められるようになります。
そのため、ポリス内のアゴラ(広場)では、集会が定期的に開かれ、平民たちが談話や議論を楽しんでいました。

ポリスどうしや外国との戦いが起こる
人が定住して人口が増えてくると、土地が足りなくなるため、各ポリスは植民市を開拓するようになります。
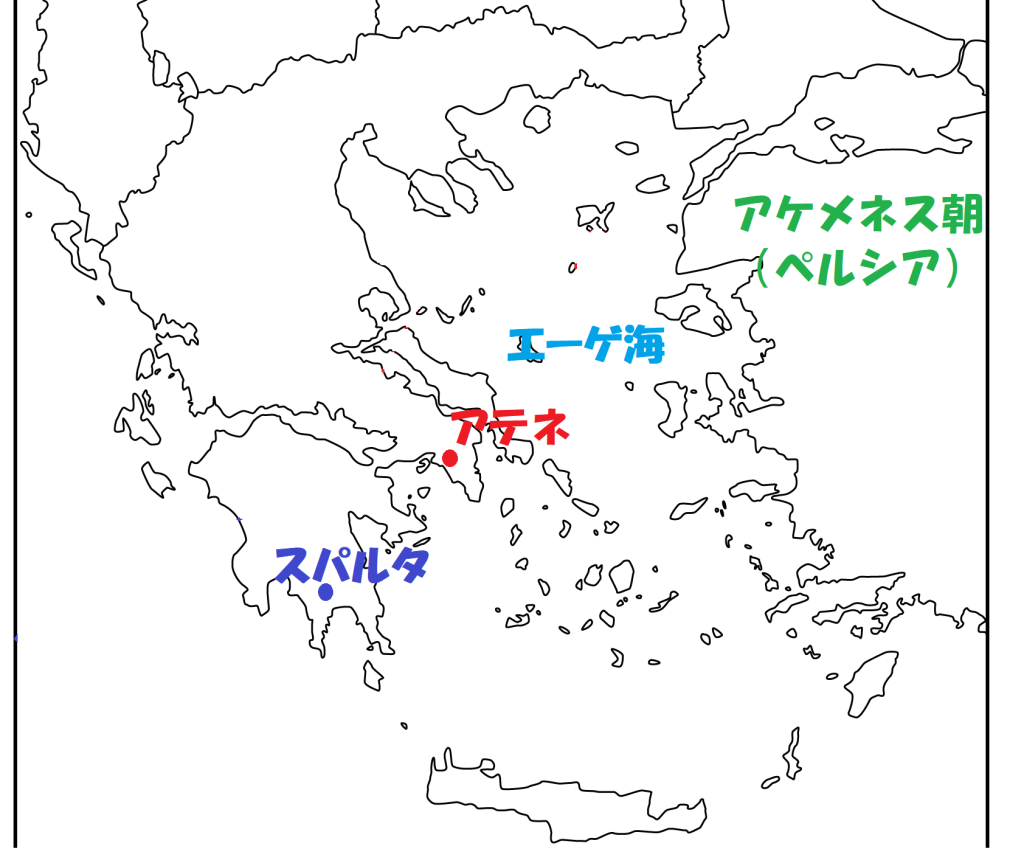
植民市が増えることでポリスの規模が拡大していき、大きな勢力を持ったのがアテネとスパルタです。
(出典:出典:白地図専門店より改変 / CC-BY-4.0)
エーゲ海を挟んだ東側では、エジプトやバビロニアといったオリエント諸国を統一したアケメネス朝(ペルシア)が勢力を持っており、この3国は頻繁に争いを繰り返しました。
- 510年※2:スパルタがアテネに侵攻。
- 508年:スパルタがアテネに再侵攻。アテネがスパルタ軍を撤退させる。
- 490年:ペルシア戦争(アテネとペルシアの戦い)が始まる。
- 480年:スパルタがペルシアに大敗する。
- :ペルシアがアテネ市内を焼きつくす。
- :アテネがペルシア艦隊を撃破する。
- 479年:スパルタがペルシア陸軍を撃破する。
- 449年:アテネとペルシアの間に平和条約が成立。
- 431年:ペロポネソス戦争(アテネとスパルタの戦い)が始まる。
- 404年:アテネに疫病が流行り、ペロポネソス戦争はスパルタの勝利。
※2 年代はすべて紀元前。
ほとんどのポリスがマケドニア支配下となる
絶え間ない戦争により、アテネやスパルタをはじめとする各ポリスは弱体化していきました。
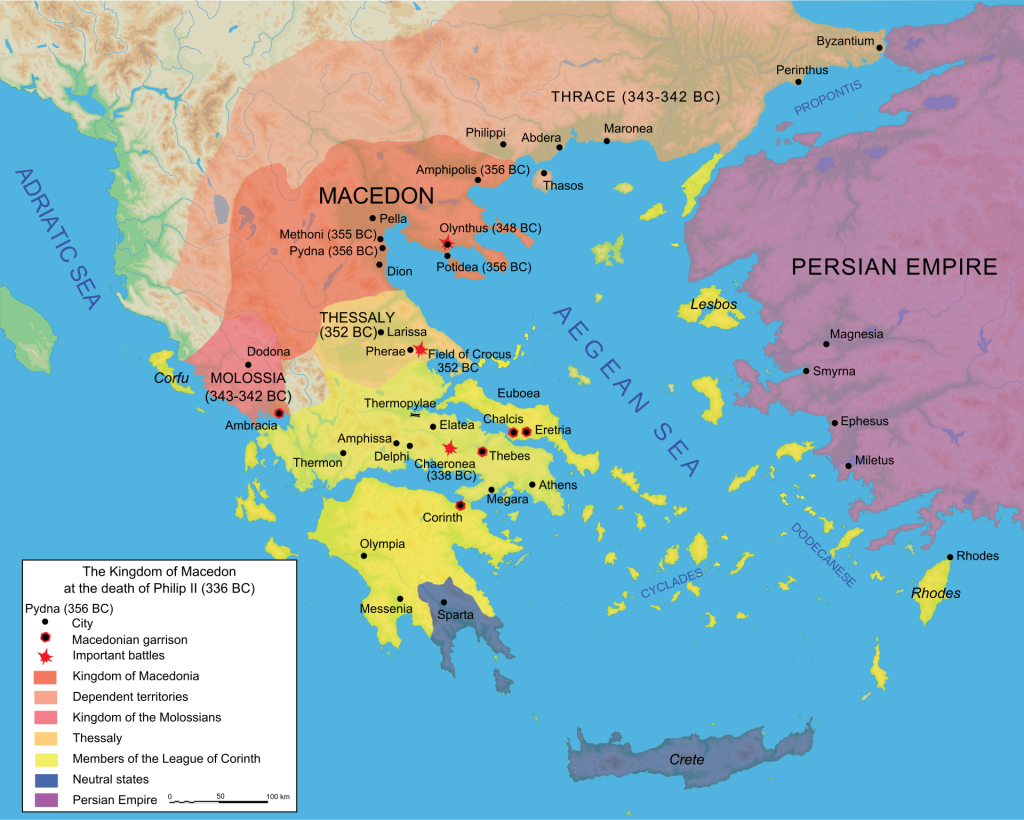
その最中に、ギリシャの北方にあるマケドニアが軍事力を徐々に強め、紀元前338年にアテネを破ります。
(出典:Map_Macedonia_336_BC-es.svg: Marsyas (French original); Kordas (Spanish translation)derivative work: MinisterForBadTimes, CC BY-SA 2.5, via Wikimedia Commons)
この出来事をきっかけに、マケドニアはギリシャのほとんどのポリスを支配下におき、ギリシャに外国の風が流れてくることになりました。
さらには、紀元前323年のマケドニアのアレクサンドロス大王急死に伴い、帝国が崩壊。
マケドニアも3つの王朝に分かれ、ギリシア時代からヘレニズム時代(~B.C.30)へと時代が変化していきます。

(出典:Giovanni Dall’Orto, Attribution, via Wikimedia Commons)
歴史が数学に与えた影響
争いが多かった古代ギリシャですが、数学が発展するうえでは良い環境が整っていたと言えます。
エジプトやバビロニアの知識が手に入った
ポリスの中でも、早いところでは紀元前8世紀半ばから植民活動をしていました。(前述)
植民市の中には、オリエントとの交易が可能な地域もあり、エジプトやバビロニアの高度な数学の知識がギリシャに伝わりました。

(出典:Paul James Cowie (Pjamescowie) / Public domain)

(出典:Bill Casselman, CC BY-SA 3.0, via Wikimedia Commons)
紀元前6世紀の数学者ピタゴラス(Pythagoras, B.C.569頃-B.C.500頃)も、若い頃にエジプトやバビロニアを旅して回り、ピタゴラスの定理(三平方の定理)を勉強しています。
「証明」の概念が生まれた
ポリスでは、市民がアゴラ(広場)で議論をする文化がありました。(前述)
議論をするうえで求められるのは、自分の主張を合理的に説明することです。

そのため、古代ギリシャ人はエジプトやバビロニアの数学的知識を鵜呑みにすることなく、それらが本当に正しいかどうかの証明を与えていきました。
他の文明では見られなかった証明という行為が、その後のギリシャ数学を発展させると共に、現在の数学にまで影響を与えています。
著作活動が活発になった
議論を大切にしていたポリスにおいては、口頭でのコミュニケーション力や記憶術が重要視されました。
そのため、プラトン(Platon , B.C.427-B.C.347)の時代まで、人や議論の内容について文字として残すという文化が無く、タレスやピタゴラスといった数学者たちの来歴や功績についても、伝聞によって語り継がれてきた情報が主となっています。

しかし、戦争の長期化によってポリスが弱体化してきた紀元前400年頃(前述)からは、先行きの不透明な世界を案じ、著作活動が活発化しました。
ギリシャ時代の数学者たちが残した研究成果は、ヘレニズム時代へと伝わり、ユークリッド(Euclid , B.C.330頃-B.C.275頃)の『原論』に総括されています。

(出典:Photograph taken by Mark A. Wilson (Wilson44691, Department of Geology, The College of Wooster).[1], Public domain, via Wikimedia Commons)
ギリシャ時代の数学者
古代エジプトやバビロニアと異なり、ギリシャ時代における数学の成果は、発見者の名前と共に残っています。
マケドニアに支配される紀元前338年までに誕生した、ギリシャ時代の数学者たちの概要を紹介します。
伝説の数学者2人
タレス(Thales , B.C.625頃~B.C.547頃)
ミレトス→エジプト→バビロニア→ミレトス→エリス地方
- 「最初の数学者」、「哲学の父」などと呼ばれる。
- 数学の定理を初めて証明した。(タレスの定理)
- その後の自然哲学に大きな影響を与えた。

(出典:Unidentified engraver, Public domain, via Wikimedia Commons)
タレスゆかりの地
ピタゴラス(Pythagoras , B.C.569頃~B.C.500頃)
サモス島→エジプト→バビロニア→サモス島→シシリー→ターレントゥム→クロトン(→メタポンティオン)
- 「三平方の定理」を初めて証明した。
- 「ピタゴラス教団」という研究グループを作った。
- 数を分類し、数のグループに名前をつけて分類した。

(出典:The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons)
ピタゴラスゆかりの地
100年以上の間、口頭で伝わってきた数学者のため、実はタレスやピタゴラスといった人物は存在しなかったという説もあります。
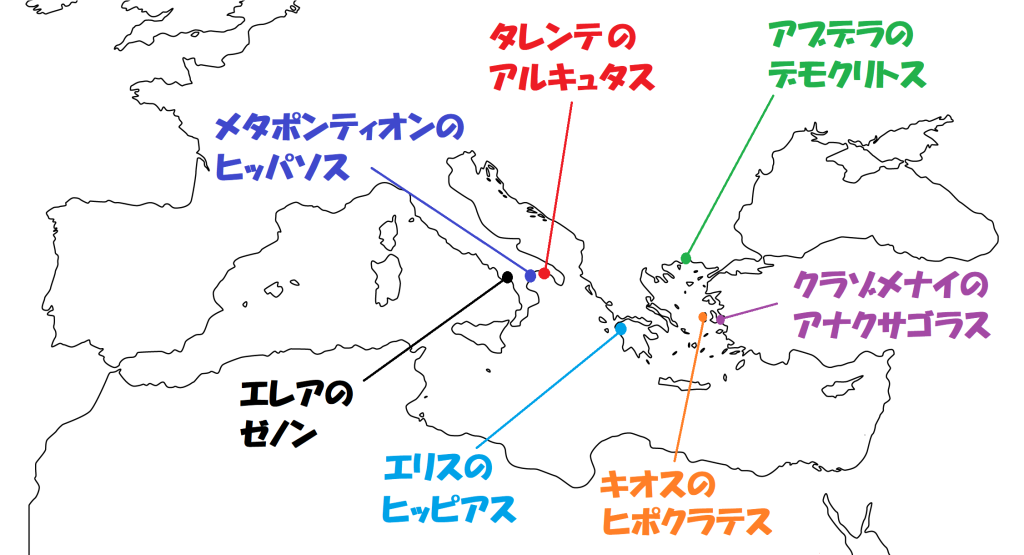
「英雄の時代」の数学者7人
紀元前5世紀は、ギリシャ数学史上「英雄の時代」と呼ばれており、以下の7人が名を連ねています。
(出典:白地図専門店より改変 / CC-BY-4.0)
アナクサゴラス(Anaxagoras , B.C.500頃~B.C.428)
クラゾメナイ→アテネ→ラムプサコス
- 円積問題に取り組んだ。
- 楕円について、初めて言及した。
- 数学的な量は無限に分割できると主張した。

(出典:Eduard Lebiedzki, after a design by Carl Rahl, Public domain, via Wikimedia Commons)
アナクサゴラスゆかりの地(Google Map・準備中)
ゼノン(Zeno , B.C.490頃~B.C.430頃)
※世界史で登場するストア派のゼノン(Zenon , B.C.335-B.C.263)とは別人物。
エレア
- 「アキレスと亀」をはじめとするパラドックスを主張した。

(出典:Jan de Bisschop, CC0, via Wikimedia Commons)
ゼノンゆかりの地(Google Map・準備中)
ヒポクラテス(Hippocrates , B.C.470頃~B.C.410頃)
※医者であり、コス島出身のヒポクラテス(Hippocrates , B.C.460頃-B.C.370頃)とは別人物。
キオス→アテネ→ビュザンティオン
- 月形を用いて、円積問題に挑戦する。
ヒポクラテスゆかりの地(Google Map・準備中)
ヒッピアス(Hippias , B.C.460頃~不明)
- 角の三等分問題を解くために、円積線を導入した。
ヒッピアスゆかりの地(Google Map・準備中)
デモクリトス(Democritus , B.C.460頃~B.C.370頃)
アブデラ→エジプト→ペルシア→バビロン→インド→アテネ→アブデラ
- 錐体の体積が、柱体の$~\displaystyle \frac{1}{3}~$であることを発表した。

(出典:Unidentified engraver, Public domain, via Wikimedia Commons)
デモクリトスゆかりの地(Google Map・準備中)
ヒッパソス(Hippasus , B.C.500頃~不明)
メタポンティオン→クロトン?
- $~\sqrt{2}~$をはじめとする、無理数の研究を行った。
- ピタゴラス教団の一員として、正五角形の作図を行った。

(出典:Boccanera G., Public domain, via Wikimedia Commons)
ヒッパソスゆかりの地(Google Map・準備中)
ギリシャ時代末期の数学者6人
ポリスの力が弱まってきたギリシア時代末期。
数学史においては、プラトンの存在によって、ギリシア数学がさらに発展を遂げました。
この時代を生きた6名の数学者を紹介します。
プラトン(Platon , B.C.427頃~B.C.347頃)
アテナイ→イタリア→エジプト→アテナイ
- アカデメイアを創設し、ギリシア学問の中心的存在となった。

(出典:Unidentified engraver, Public domain, via Wikimedia Commons)
プラトンゆかりの地(Google Map・準備中)
テアイテトス(Theaetetus , B.C.415頃~B.C.369)
アテナイ→コリントス
- $~\sqrt{2}~$や$~\sqrt{3}~$といった平方根の概念を研究した。
テアイテトスゆかりの地(Google Map・準備中)
エウドクソス(Eudoxus , B.C.408頃~B.C.355頃)
クニドス→アテナイ→エジプト→アテナイ
- 比例論によって、2つの量の比の相等を定義した。
- 汲み尽くし法を考えた。
エウドクソスゆかりの地(Google Map・準備中)
ディノストラトス(Dinostratus , B.C.390頃~B.C.320頃)
ギリシア
- 立方体倍積問題を、3次元の作図によって解いた。
- 調和平均を定義した。
ディノストラトスゆかりの地(Google Map・準備中)
メナイクモス(Menaechmus , B.C.380頃~B.C.320頃)
ギリシア→アロペコネソス
- 立方体倍積問題を解決するため、円錐曲線を発見した。
メナイクモスゆかりの地(Google Map・準備中)
アリストテレス(Aristoteles , B.C.384頃~B.C.322)
スタゲイラ→アテナイ→アッソス→ミュティレネ→ペラ→アテナイ→カルキス
- 証明の手法や言葉をまとめ、数学の学問モデルを確立した。
- リュケイオンを創設した。

(出典:After Lysippos, Public domain, via Wikimedia Commons)
アリストテレスゆかりの地(Google Map・準備中)
アリストテレスは、マケドニアのアレクサンドロス大王の家庭教師をしていたため、当時の学問に大きな影響力を持っていました。
しかし、紀元前323年にアレクサンドロス大王が急死すると、アリストテレスの影響力も弱まり、翌年にアリストテレス自身も亡くなっています。
そのため、文明史においては、アレクサンドロス大王の死がギリシャ時代とヘレニズム時代を分ける境界線となっているのです。
まとめ
古代ギリシャの中でも、ギリシャ時代(~B.C.323)における歴史と数学者について解説をしました。
- ポリスの市民の議論好きな文化が、数学における証明を誕生させた。
- タレスやピタゴラスをはじめとする数学者たちの名が、功績と共に現在にまで残っている。
- ギリシャ時代は、アレクサンドロス大王とアリストテレスの死によって終焉を迎えた。
次の記事以降では、ギリシャ時代の数学の中身を見ていきます。


数学者の名前が、プラトンとユークリッド以外、全員「〇〇ス」だ!



プラトンの本名は「アリストクレス」、ユークリッドが「エウクレイデス」だよ。
その時代の文法に従っていたんだ。
ただ、ゼノンだけは特殊だね。
参考文献(本の紹介ページにリンクしています)
- 『カッツ 数学の歴史』,pp.55-118
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,pp.41-98
- 『数学史 数学5000年の歩み』,pp.83-119
- 『数学の歴史物語』,pp.41-76
- 『数学の流れ30講(上)』,pp.25-55
- 『世界数学者事典』
- マイケル・J・ブラッドリー(2009)『数学を切りひらいた人びと1-数学を生んだ父母たち』,pp.14-48
- ピエルジョルジョ・オーディフレッディ著,河合成雄訳(2021)『幾何学の偉大なものがたり』,pp55-118



コメント