１辺の長さが$~a~$となる正$~n~$角形の面積を求めます。
$~n~$を大きくしていくと・・・。
- 正$~n~$角形の面積の公式
- 公式の使い方
- 公式の証明
Ⅰ 面積の公式
正$~n~$角形の面積が、どのような公式で表されるのかをまずは見てみましょう。
１辺の長さが $~a~$ である正 $~n~$ 角形の面積 $~S_n~$ は、次の公式で求められる。
\begin{equation*}
S_n=\frac{na^2}{4 \tan{\frac{\pi}{n}}}
\end{equation*}意外ときれいな式となっているのではないでしょうか。
ただ、分母に$~\tan{}~$がありますので、その値が出るような$~n~$でないと正確な面積は求まりません。
Ⅱ 例
では、実際に$~\displaystyle \tan{\frac{\pi}{n}}~$の値がわかる$~n~$をいくつか代入して、正$~n~$角形の面積を公式から計算してみましょう。
\begin{equation*}
\tan{\frac{\pi}{4}}=\tan{45^{\circ}}=1
\end{equation*}より、１辺の長さが$~a~$の正三角形の面積は、
\begin{align*}
S_4&=\displaystyle \frac{4 \cdot a^2}{4 \cdot 1} \\
\\
&=a^2
\end{align*}と求まる。
正四角形、すなわち正方形をこの公式で求める人はまずいないでしょうw
ただ、しっかりと縦×横と同じ答えが出ました。
36°の三角比より、
\begin{equation*}
\tan{\frac{\pi}{5}}=\tan{36^{\circ}}=\sqrt{5-2\sqrt{5}}
\end{equation*}より、１辺の長さが$~a~$の正五角形の面積は、
\begin{align*}
S_5&=\frac{5 \cdot a^2}{4 \cdot \sqrt{5-2\sqrt{5}}} \\
\\
&=\frac{5 \cdot \sqrt{5+2\sqrt{5}}}{4 \cdot \sqrt{5-2\sqrt{5}}\sqrt{5+2\sqrt{5}}}a^2 \\
\\
&=\frac{5 \cdot \sqrt{5+2\sqrt{5}}}{4 \cdot \sqrt{25-20}}a^2 \\
\\
&=\frac{5 \cdot \sqrt{5+2\sqrt{5}}}{4 \cdot \sqrt{5}}a^2 \\
\\
&=\frac{\sqrt{5} \cdot \sqrt{5+2\sqrt{5}}}{4}a^2 \\
\\
&=\frac{\sqrt{25+10\sqrt{5}}}{4}a^2
\end{align*}と求まる。
「コレ、本当に正しいのか？」と思われた方は、他の求め方もありますので是非ご覧ください↓
18°の三角比より、
\begin{equation*}
\tan{\frac{\pi}{12}}=\tan{18^{\circ}}=2-\sqrt{3}
\end{equation*}より、１辺の長さが$~a~$の正十二角形の面積は、
\begin{align*}
S_{12}&=\displaystyle \frac{12 \cdot a^2}{4 \cdot (2-\sqrt{3})} \\
\\
&=\frac{3(2+\sqrt{3})}{(2-\sqrt{3})(2+\sqrt{3})}a^2 \\
\\
&=\frac{6+3\sqrt{3}}{4-3}a^2 \\
\\
&=(6+3\sqrt{3})a^2
\end{align*}と求まる。
三角比の値が、手計算でわかる$~n~$の値は、$~n=3,4,5,6,8,10,12~$あたりなので、それらから抜粋して例を挙げました。
次の章では、いよいよ公式の証明に入ります。
Ⅲ 面積の公式（一般化）の証明
証明で利用するのは外接円です
正$~n~$角形の中心$~O~$と各頂点を結ぶことによってできる、$~n~$個の二等辺三角形について考える。
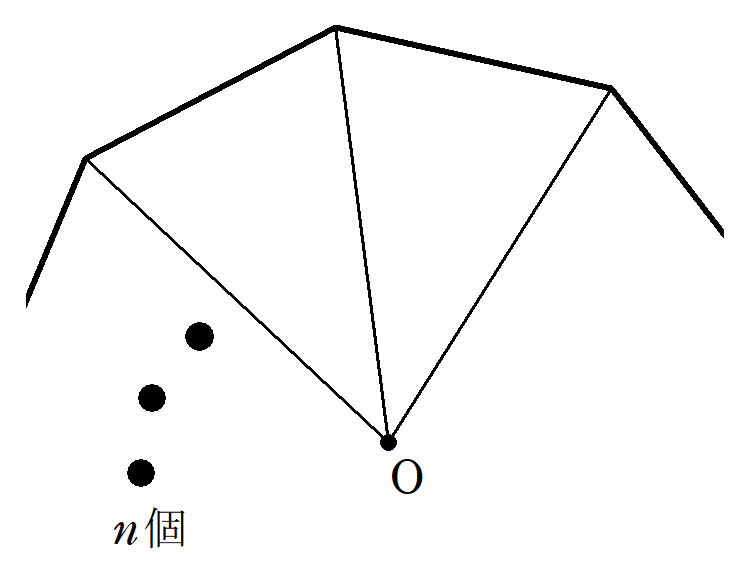
その二等辺三角形の中の１つを$~\triangle OAB~$とし、下の図のような、正$~n~$角形の外接円を考える。
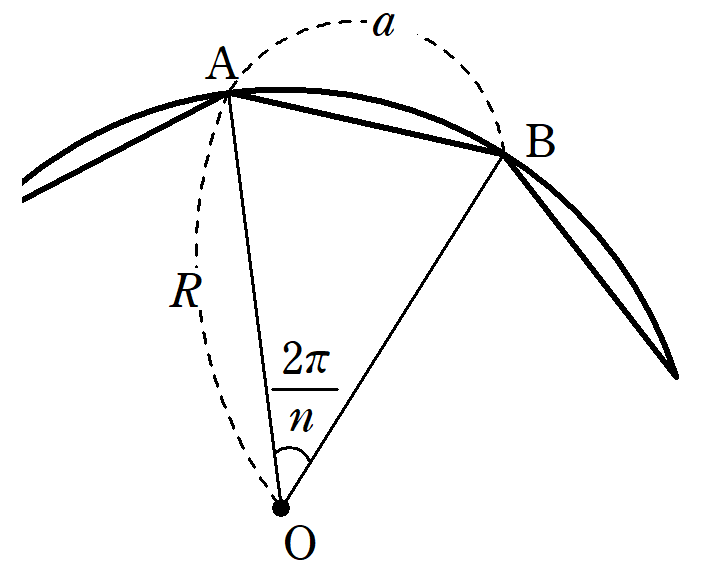
この外接円の半径を$~R~$とすると、
\begin{align*}
\triangle OAB&=\frac{1}{2}\cdot R \cdot R \cdot \sin{\frac{2\pi}{n}} \\
\\
&=\frac{1}{2}R^2 \sin{\frac{2\pi}{n}}~~~~~~\cdots ①
\end{align*}と表せる。
ここで、$~R~$を$~a~$で表すために、$~O~$から$~AB~$へ垂線$~OH~$を引く。
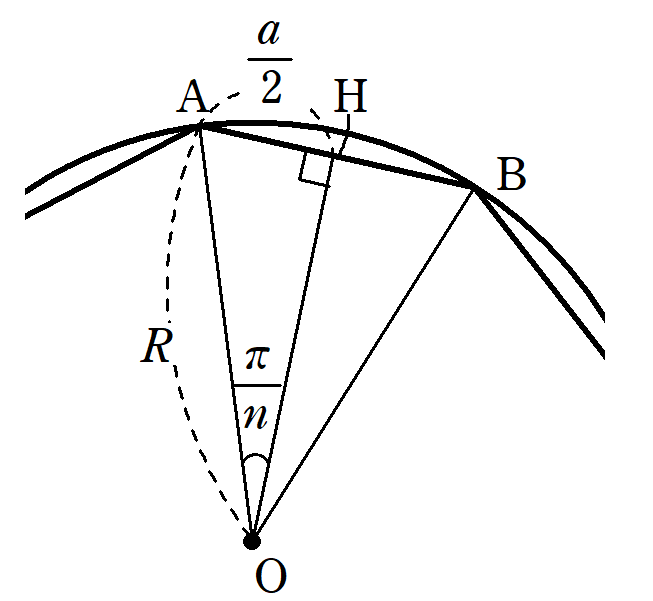
$~\triangle OAH~$で、正弦の定義より、
\begin{align*}
\sin{\frac{\pi}{n}}&=\frac{\frac{1}{2}a}{R} \\
\\
R&=\frac{a}{2\sin{\frac{\pi}{n}}} ~~~~\cdots ②
\end{align*}となるため、$②$を$①$に代入し、２倍角の公式を使って式変形していくと、
\begin{align*}
\triangle OAB&=\frac{1}{2}\left( \frac{a}{2\sin{\frac{\pi}{n}}} \right)^2 \cdot \sin{\frac{2\pi}{n}} \\
\\
&=\frac{1}{2} \cdot \frac{a^2}{4\sin^2{\frac{\pi}{n}}} \cdot 2\sin{\frac{\pi}{n}} \cos{\frac{\pi}{n}} \\
\\
&=\frac{a^2}{4\sin{\frac{\pi}{n}}}\cdot \cos{\frac{\pi}{n}} \\
\\
&=\frac{a^2}{4\frac{\sin{\frac{\pi}{n}}}{\cos{\frac{\pi}{n}}}} \\
\\
&= \frac{a^2}{4\tan{\frac{\pi}{n}}}{n}
\end{align*}が求まる。
正$~n~$角形は、$~\triangle OAB~$$~n~$個分なので、
\begin{align*}
S_n&= \frac{na^2}{4\tan{\frac{\pi}{n}}}
\end{align*}という式になる。■
外接円の中心角をうまく用いた考え方でした。
Ⅳ 円の面積へ
余談ですが、①の式の極限を考えることで、円の面積を求めることもできます。
正$~n~$角形の面積を$~R~$を使って表すと、$①$より、
\begin{align*}
S_n&=\frac{1}{2} R^2 \sin{\frac{2\pi}{n}} \cdot n \\
\\
&=\frac{1}{2} n \sin{\frac{2\pi}{n}} \cdot R^2
\end{align*}と表せる。
$~n~$を$~+\infty~$に近づけたとき、
\begin{align*}
\lim_{n \to \infty}S_n&=\lim_{n \to \infty} \frac{1}{2}\cdot \frac{ \sin{\frac{2\pi}{n}}}{\frac{1}{n}} \cdot R^2 \\
\\
&=\lim_{n \to \infty} \frac{1}{2}\cdot \frac{ \sin{\frac{2\pi}{n}}}{\frac{1}{2\pi}\cdot \frac{2 \pi}{n}} \cdot R^2 \\
\\
&=\lim_{n \to \infty} \pi \cdot \frac{ \sin{\frac{2\pi}{n}}}{\frac{2 \pi}{n}} \cdot R^2
\end{align*}と変形でき、$~\displaystyle \frac{2 \pi}{n}=t~$とすると、
\begin{align*}
&=\lim_{t \to 0} \pi \cdot \frac{\sin{t}}{t} \cdot R^2 \\
\\
&=\pi \cdot 1 \cdot R^2 \\
\\
&=\pi R^2
\end{align*}が求まる。これは円の面積を表している。
$~n~$を大きくしていけばいくほど、確かに外接円に近づいていきます。↓↓
この方法を利用して、円周率の近似に挑んだのが、ドイツ生まれの数学者ファン・ケーレン・ルドルフ（Van Ceulen Ludolph , 1540-1610）です。
彼は正$~2^{62}~$角形を使って、円周率を35桁まで正確に割り出しました。
正$~2^{62}~$角形って、どのくらい？
おおよそだけど、正400京角形だね。
絶対に円と見分けがつかない。
コメント