一辺の長さを$~a~$としたとき、正三角形や正五角形の面積がどう表されるかを知っていますか?
実は、一辺$~a~$の正$~n~$角形の面積をまとめて表す公式があります!
その公式とは、$~\displaystyle S_n=\frac{na^2}{4 \tan{\frac{\pi}{n}}}~$で、$~\tan{}~$の値が求まる限り、どんな$~n~$でも使えます。
この記事では、公式の求め方やそこから求まる正多角形の面積を、現役数学教員がわかりやすく解説しています。
高校受験や大学受験における幾何問題のスピードアップに役立てましょう!
- 正$~n~$角形の面積の公式
- 公式の証明方法
- 公式を使った面積の求め方
- $~n~$を大きくしていくと、円になる!?
正 n 角形の面積の公式
公式の内容
正$~n~$角形の面積は、以下の公式で求めることができます。
1辺の長さが $~a~$ である正 $~n~$ 角形の面積 $~S_n~$ は、次の公式で求められる。
S_n=\frac{na^2}{4 \tan{\frac{\pi}{n}}}意外ときれいな式となっているのではないでしょうか。
ただ、分母に$~\tan{}~$があるので、その値が出るような$~n~$でないと正確な面積は求まりません。
公式の証明
証明は、外接円を利用することで行うことができます。
正$~n~$角形の中心$~O~$と各頂点を結ぶことによってできる、$~n~$個の二等辺三角形について考える。
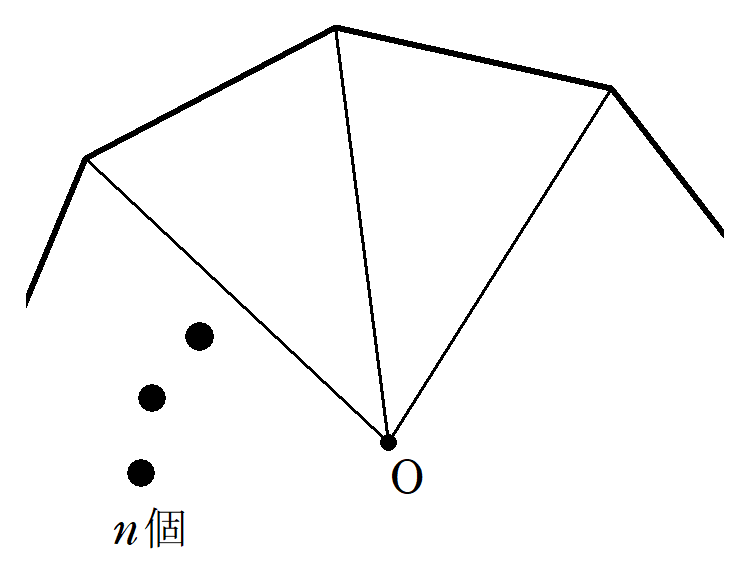
その二等辺三角形の中の1つを$~\triangle OAB~$とし、下の図のような、正$~n~$角形の外接円を考える。
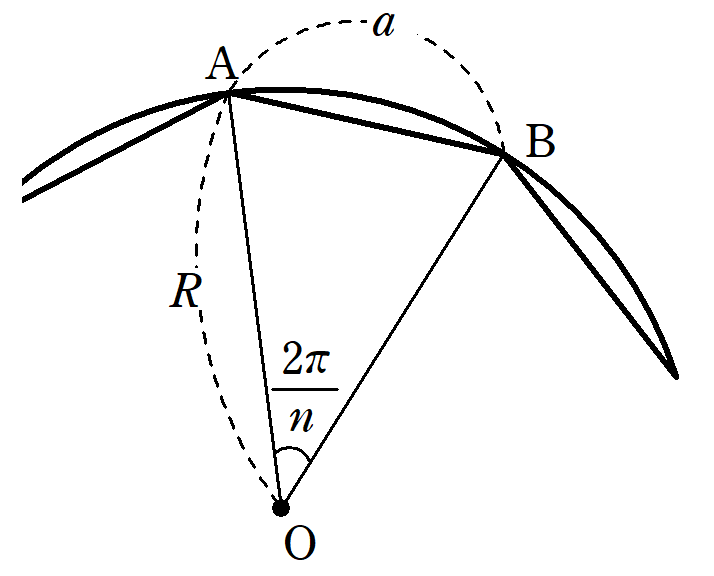
この外接円の半径を$~R~$とすると、
\begin{align*}
\triangle OAB&=\frac{1}{2}\cdot R \cdot R \cdot \sin{\frac{2\pi}{n}} \\
\\
&=\frac{1}{2}R^2 \sin{\frac{2\pi}{n}}~~~~~~\cdots ①
\end{align*}と表せる。
ここで、$~R~$を$~a~$で表すために、$~O~$から$~AB~$へ垂線$~OH~$を引く。
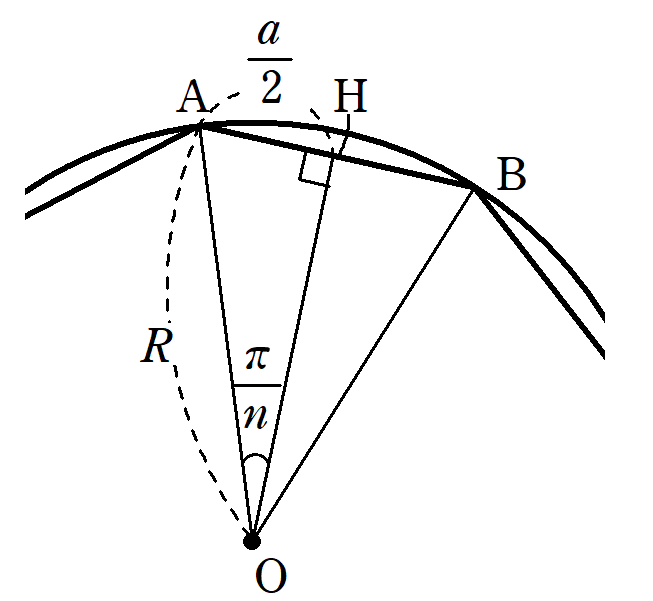
$~\triangle OAH~$で、正弦の定義より、
\begin{align*}
\sin{\frac{\pi}{n}}&=\frac{\frac{1}{2}a}{R} \\
\\
R&=\frac{a}{2\sin{\frac{\pi}{n}}} ~~~~\cdots ②
\end{align*}となるため、$②$を$①$に代入し、2倍角の公式を使って式変形していくと、
\begin{align*}
\triangle OAB&=\frac{1}{2}\left( \frac{a}{2\sin{\frac{\pi}{n}}} \right)^2 \cdot \sin{\frac{2\pi}{n}} \\
\\
&=\frac{1}{2} \cdot \frac{a^2}{4\sin^2{\frac{\pi}{n}}} \cdot 2\sin{\frac{\pi}{n}} \cos{\frac{\pi}{n}} \\
\\
&=\frac{a^2}{4\sin{\frac{\pi}{n}}}\cdot \cos{\frac{\pi}{n}} \\
\\
&=\frac{a^2}{4\frac{\sin{\frac{\pi}{n}}}{\cos{\frac{\pi}{n}}}} \\
\\
&= \frac{a^2}{4\tan{\frac{\pi}{n}}}{n}
\end{align*}が求まる。
正$~n~$角形は、$~\triangle OAB~$$~n~$個分なので、
\begin{align*}
S_n&= \frac{na^2}{4\tan{\frac{\pi}{n}}}
\end{align*}という式になる。■
2倍角の公式を使っているため、証明に関しては数学Ⅱの知識まで必要となります。
さまざまな正多角形の公式
公式一覧
正$~n~$角形の面積の公式を使えば、$~n=3~,~4~,~5~,~6~,~8~,~10~,~12~$のときに、近似値を使わずに公式を与えることができます。
1辺の長さが $~a~$ である、次の正$~n~$角形の面積$~S_n~$は、次の公式で求められる。
\begin{align*}
S_3&=\frac{\sqrt{3}}{4}a^2 \\
\\
S_4&=a^2 \\
\\
S_5&=\frac{\sqrt{25+10\sqrt{5}}}{4}a^2 \\
\\
S_6&=\frac{3\sqrt{3}}{2}a^2 \\
\\
S_8&=2(\sqrt{2}+1)a^2 \\
\\
S_{10}&=\frac{\sqrt{5}\sqrt{25+10\sqrt{5}}}{2}a^2 \\
\\
S_{12}&=3(2+\sqrt{3})a^2
\end{align*}マニアックではありますが、$~\displaystyle \tan{\frac{\pi}{5}}=\tan{36^{\circ}}=\sqrt{5-2\sqrt{5}}~$などの三角比の値を代入することで、以上のように面積を求めることができます。
三角比の値については、以下の記事を参照してください。
正四角形($~S_4~$)の面積の公式は当たり前として、正三角形 ($~S_3~$)の面積は高校受験や大学受験でよく使うので覚えてしまいましょう。
公式の導出
正$~n~$角形の面積の公式からいろいろな正多角形の面積 が導かれるまでの計算過程を示しておきます。
三角比の値を代入し、必要に応じて有理化や約分を行うだけ求まります。
・正三角形
\tan{\frac{\pi}{3}}=\tan{60^{\circ}}=\sqrt{3}より、1辺の長さが$~a~$の正三角形の面積は、
\begin{align*}
S_3&=\frac{3 \cdot a^2}{4 \cdot \sqrt{3}} \\
\\
&=\frac{3\sqrt{3}}{4 \cdot 3}a^2 \\
\\
&=\frac{\sqrt{3}}{4}a^2 \\
\end{align*}と求まる。■
・正四角形(正方形)
\tan{\frac{\pi}{4}}=\tan{45^{\circ}}=1より、1辺の長さが$~a~$の正四角形の面積は、
\begin{align*}
S_4&=\frac{4 \cdot a^2}{4 \cdot 1} \\
\\
&=a^2
\end{align*}と求まる。■
・正五角形
36°の三角比より、
\tan{\frac{\pi}{5}}=\tan{36^{\circ}}=\sqrt{5-2\sqrt{5}}より、1辺の長さが$~a~$の正五角形の面積は、
\begin{align*}
S_5&=\frac{5 \cdot a^2}{4 \cdot \sqrt{5-2\sqrt{5}}} \\
\\
&=\frac{5 \cdot \sqrt{5+2\sqrt{5}}}{4 \cdot \sqrt{5-2\sqrt{5}}\sqrt{5+2\sqrt{5}}}a^2 \\
\\
&=\frac{5 \cdot \sqrt{5+2\sqrt{5}}}{4 \cdot \sqrt{25-20}}a^2 \\
\\
&=\frac{5 \cdot \sqrt{5+2\sqrt{5}}}{4 \cdot \sqrt{5}}a^2 \\
\\
&=\frac{\sqrt{5} \cdot \sqrt{5+2\sqrt{5}}}{4}a^2 \\
\\
&=\frac{\sqrt{25+10\sqrt{5}}}{4}a^2
\end{align*}と求まる。■
・正六角形
\tan{\frac{\pi}{6}}=\tan{30^{\circ}}=\frac{1}{\sqrt{3}}より、1辺の長さが$~a~$の正六角形の面積は、
\begin{align*}
S_6&=\frac{6 \cdot a^2}{4 \cdot \frac{1}{\sqrt{3}}} \\
\\
&=\frac{6 \cdot \sqrt{3}}{4 \cdot \frac{1}{\sqrt{3}}\cdot \sqrt{3}}a^2 \\
\\
&=\frac{3\sqrt{3}}{2}a^2 \\
\end{align*}と求まる。■
・正八角形
22.5°の三角比より、
\tan{\frac{\pi}{8}}=\tan{22.5^{\circ}}=\sqrt{2}-1より、1辺の長さが$~a~$の正八角形の面積は、
\begin{align*}
S_8&=\frac{8 \cdot a^2}{4(\sqrt{2}-1)} \\
\\
&=\frac{2}{\sqrt{2}-1}a^2 \\
\\
&=\frac{2(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}a^2 \\
\\
&=\frac{2(\sqrt{2}+1)}{2-1}a^2 \\
\\
&=2(\sqrt{2}+1)a^2
\end{align*}と求まる。■
・正十角形
18°の三角比より、
\tan{\frac{\pi}{10}}=\tan{18^{\circ}}=\frac{\sqrt{25-10\sqrt{5}}}{5}より、1辺の長さが$~a~$の正十角形の面積は、
\begin{align*}
S_{10}&=\frac{10 \cdot a^2}{4 \cdot \frac{\sqrt{25-10\sqrt{5}}}{5}} \\
\\
&=\frac{10 \cdot 5}{4 \cdot \frac{\sqrt{25-10\sqrt{5}}}{5}\cdot 5}a^2 \\
\\
&=\frac{50}{4\sqrt{25-10\sqrt{5}}}a^2 \\
\\
&=\frac{25 \cdot \sqrt{25+10\sqrt{5}}}{2 \cdot\sqrt{25-10\sqrt{5}}\sqrt{25+10\sqrt{5}}}a^2 \\
\\
&=\frac{25 \sqrt{25+10\sqrt{5}}}{2\sqrt{625-500}}a^2 \\
\\
&=\frac{25 \sqrt{25+10\sqrt{5}}}{2\cdot 5\sqrt{5}}a^2 \\
\\
&=\frac{\sqrt{5} \sqrt{25+10\sqrt{5}}}{2}a^2 \\
\end{align*}と求まる。■
・正十二角形
15°の三角比より、
\begin{equation*}
\tan{\frac{\pi}{12}}=\tan{15^{\circ}}=2-\sqrt{3}
\end{equation*}より、1辺の長さが$~a~$の正十二角形の面積は、
\begin{align*}
S_{12}&=\displaystyle \frac{12 \cdot a^2}{4 \cdot (2-\sqrt{3})} \\
\\
&=\frac{3(2+\sqrt{3})}{(2-\sqrt{3})(2+\sqrt{3})}a^2 \\
\\
&=\frac{3(2+\sqrt{3})}{4-3}a^2 \\
\\
&=3(2+\sqrt{3})a^2
\end{align*}と求まる。■
三角比をもっと細かくしていけば、複雑ではありますが、正二十四角形などの面積も求めることができます。
n を大きくしていくと、円に近づく!?
余談ですが、公式の証明で出てきた$①$の$~n~$を無限に大きくすることで、円の面積を求めることもできます。
正$~n~$角形の外接円の半径を$~R~$とすると、$~n~$個に分割された$~\triangle OAB~$の面積は、
\triangle OAB=\frac{1}{2}R^2 \sin{\frac{2\pi}{n}}~~~\cdots ①と表されました。

これを$~n~$個組み合わせれば、正$~n~$角形になり、その面積で極限を考えてみます。
正$~n~$角形の面積を、外接円の半径$~R~$を使って表すと、$①$より、
\begin{align*}
S_n&=\frac{1}{2} R^2 \sin{\frac{2\pi}{n}} \cdot n \\
\\
&=\frac{1}{2} n \sin{\frac{2\pi}{n}} \cdot R^2
\end{align*}と表せる。
$~n~$を$~+\infty~$に近づけたとき、
\begin{align*}
\lim_{n \to \infty}S_n&=\lim_{n \to \infty} \frac{1}{2}\cdot \frac{ \sin{\frac{2\pi}{n}}}{\frac{1}{n}} \cdot R^2 \\
\\
&=\lim_{n \to \infty} \frac{1}{2}\cdot \frac{ \sin{\frac{2\pi}{n}}}{\frac{1}{2\pi}\cdot \frac{2 \pi}{n}} \cdot R^2 \\
\\
&=\lim_{n \to \infty} \pi \cdot \frac{ \sin{\frac{2\pi}{n}}}{\frac{2 \pi}{n}} \cdot R^2
\end{align*}と変形でき、$~\displaystyle \frac{2 \pi}{n}=t~$とすると、
\begin{align*}
&=\lim_{t \to 0} \pi \cdot \frac{\sin{t}}{t} \cdot R^2 \\
\\
&=\pi \cdot 1 \cdot R^2 \\
\\
&=\pi R^2
\end{align*}が求まる。これは円の面積を表している。
$~n~$を大きくしていけばいくほど、確かに外接円に近づいていきます。↓↓
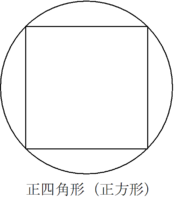
ただ、この方法で円周率の近似値を求めようとするのは、三角比の値が複雑であることから、非現実的です。

公式自体は意外とシンプルだね。



曲者は$~\tan{}~$だよね。$~n~$が大きくなるほど、多重根号のオンパレードだよ。
コメント