競技場のパラドックスは、二分法、アキレスと亀、飛んでいる矢と並び、古代ギリシャの哲学者ゼノンが提起したパラドックスの中の一つです。
この記事では、
- このパラドックスがどのようにして提起されたのか
- どのような内容のパラドックスで、どこに問題があるのか
- パラドックスをどのように解決すればよいのか
という疑問を解消するため、競技場のパラドックスを具体例を用いて、現役数学教員がわかりやすく解説しています。
このパラドックスは、ゼノンの有名な4つのパラドックスで一番わかりづらいものの、相対速度の考え方を適用するだけで論破できます!
競技場のパラドックスとは?
競技場のパラドックスは、別名「スタジアム(スタジオン)のパラドックス」とも呼ばれます。
ただ、実際はあまり競技場の要素はなく、すれ違いについての内容となっています。

哲学者ゼノンが提起したパラドックスの1つ
競技場のパラドックスを提起したのは、紀元前5世紀頃の哲学者ゼノン(Zeno , B.C.490頃-B.C.430頃)です。
「飛んでいる矢のパラドックス」と同様、時間の最小単位は瞬間であると主張するミレトス学派を批判するために、今回のパラドックスを提起しました。

(出典:Jan de Bisschop, CC0, via Wikimedia Commons)
 ゼノン
ゼノン飛んでいる矢のパラドックスで瞬間の存在を否定したから、今回は「時間の最小単位」という考え方自体を否定してみせよう。
最小の時間の単位はないことを示した
では、競技場のパラドックスの中身の説明に入ります。
4つの同じ大きさのブロックがつながってできた$~A~,~B~,~C~$のブロック列がある。
$~A~$は静止しており、$~B~$は左から右に動き、$~C~$は$~B~$と同じ速さで右から左に動く。
$~B~$と$~C~$が1ブロック分動く時間を、最小単位時間として、図3の状態から図4の状態への遷移を考える。
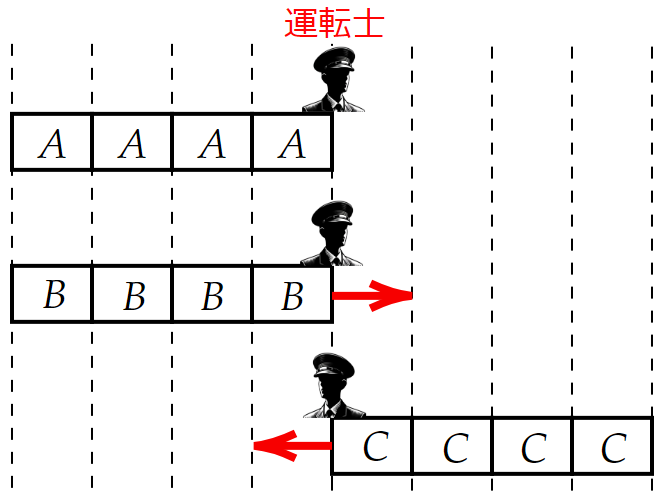

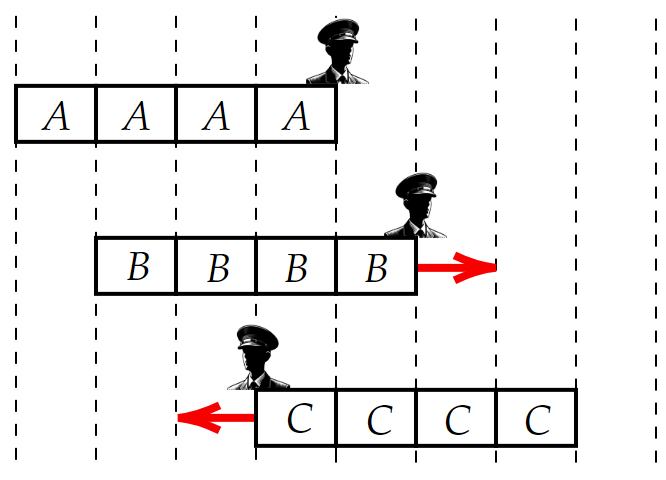

このとき、$~B~$から見て$~A~$はブロック$~1~$個分動いて見えるため、最小単位時間しか流れていないことに納得できる。(図5)
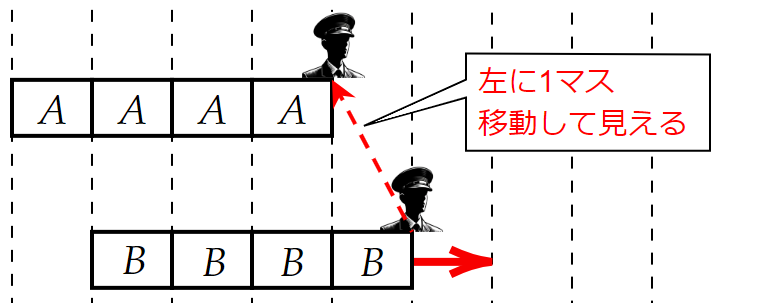

しかし、$~B~$から見て$~C~$はブロック$~2~$個分動いて見えるため、最小単位時間の2倍の時間が流れたことになる。(図6)
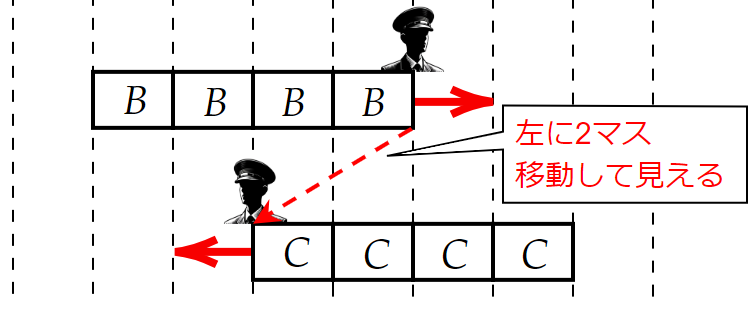

これは最小単位時間ではなくなってしまうため、最小単位時間という設定に矛盾。
そのため、最小単位時間という概念は存在しない。
他の3つのパラドックスに比べて内容が難しいですが、要するに時間の最小単位を決めたはずがいつの間にか最小でなくなっていたということを指しています。



時間の根源を「瞬間」としたミレトス学派よ、そもそも時間の最小単位という考え方(時間の根源を探す考え方)は論外なのだ!


パラドックスから1=2も示せる
このパラドックスに反論できないとすると、数学の秩序の危機に陥ってしまいます。
なぜなら、競技場のパラドックスでは、最小単位時間$~1~$が、その$~2~$倍の時間と等しくなっているため、
1=2
が成り立ってしまうのです。


競技場のパラドックスはどう解決されるのか?
ゼノンの他の3つのパラドックスと比べ、解決の方法はそんなに難しくありません。
走っている電車の窓から、止まっている電車を見るのと、逆方向から走ってくる電車を見るときとで、速さに違いを感じたことがあるはずです。
この違いを数値化しましょう。
相対速度の考え方で解決できる
鍵となるのは、相対速度という考え方。次のような式で求めることができます。
相対速度=(相手の速度)-(自分の速度)
ただし、速度は符号付きの速さを表す。(右向きの速さを$~+~$とすれば、左向きの速さは$~-~$で表される)
相対速度を使って、競技場のパラドックスを見てみると、時間がずれているのではなく、速さがずれていることが数値としてわかります。
ブロック列$~B~$の速さを$~+1~マス/\Delta t~~~~(~\Delta t~$は最小単位時間$~)~$とすると、$~A~$の速さは$~0~マス/\Delta t~$、$~C~$の速さは$~-1~マス/\Delta t~$と表すことができる。
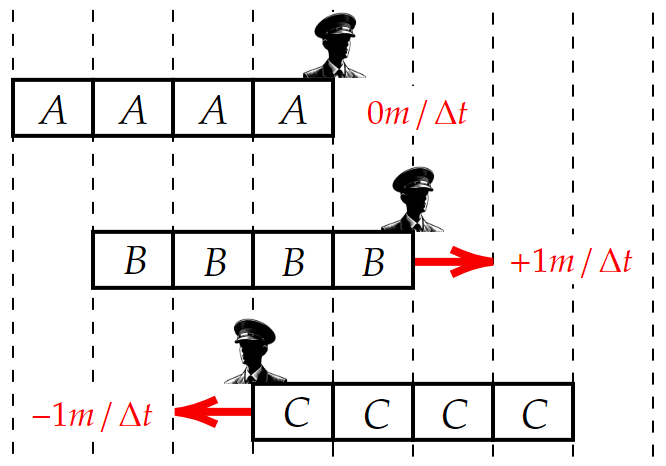

$~B~$から見た$~C~$の相対速度は、$~(-1)-(+1)=-2~マス/\Delta t~$。
$~B~$から見た$~A~$の相対速度は、$~0-(+1)=-1~マス/\Delta t~$。
よって、最小単位時間$~\Delta t~$あたりに進めるマスに$~2~$倍の違いがあることがわかる。
このパラドックスに関しては、ゼノンの約100年後の哲学者アリストテレス(Aristotle , B.C.384~B.C.322)も著書の『自然学』の中で論破しています。


(出典:Lysippos , public domain, via Wikimedia Commons)
他の3つのパラドックスの解決が17世紀であることと比較すると、競技場のパラドックスの解決が簡単であったことがわかります。



走ってみれば速度の違いがわかるっしょ。
まとめ:実際の速さと見た目の速さは違う
競技場のパラドックスについて解説をしてきました。
- 古代ギリシャの哲学者ゼノンが、ミレトス学派の「時間に最小単位がある」という考えに対抗するために提起した。
- 相対速度の違いがパラドックスの原因である。



内容を理解するまで大変だけど、解決はしやすいパラドックスだったよ。



無限との絡みが薄いから、直感で誤りに気付きやすいよね。
参考文献
- 『カッツ 数学の歴史』,pp.68-69.
- 『メルツバッハ&ボイヤー数学の歴史Ⅰー数学の萌芽から17世紀前期までー』,pp.72-74.
- 『数学の流れ30講(上)ー16世紀までー』,pp.28-31.
- 『数学の歴史物語』,pp.46-47.
- 『世界数学者事典』,pp.252-253.
- 『ギリシャ数学史』,pp.154-155.
- 『アキレスとカメーパラドックスの考察ー』,pp90-91.

コメント