教科書数学– category –
-

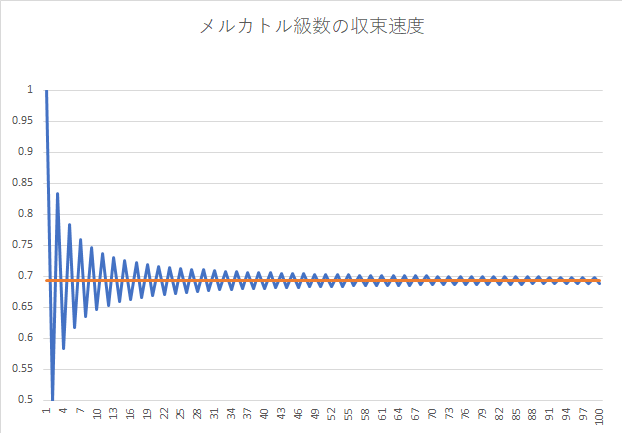
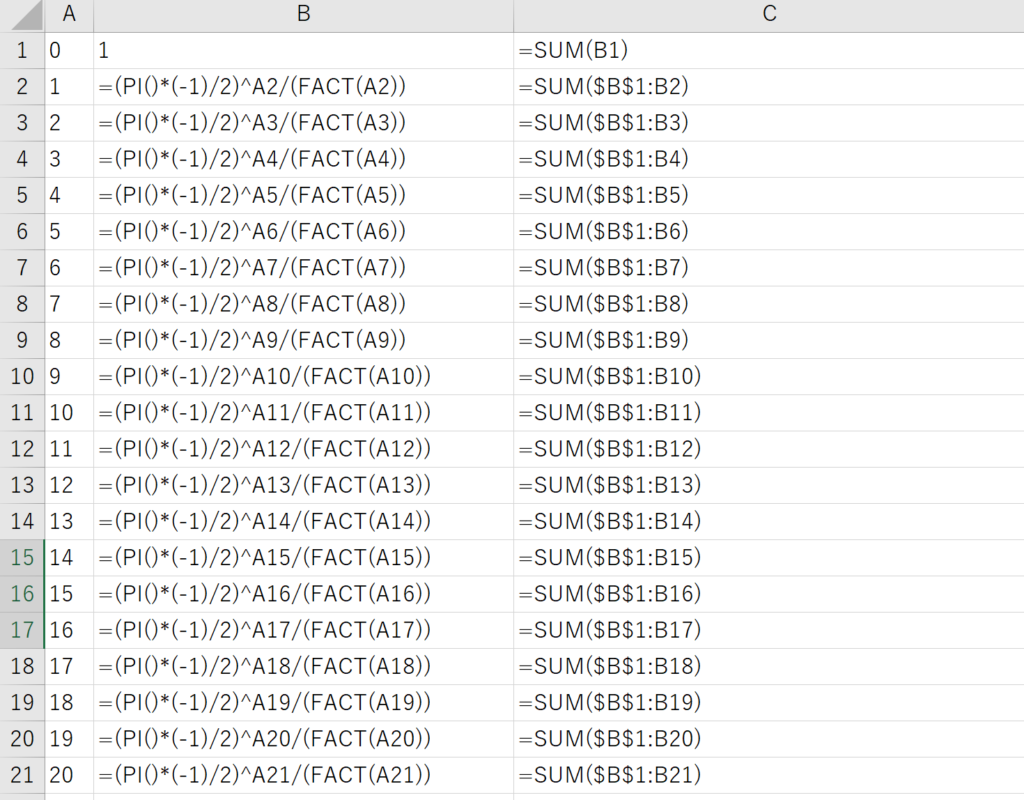
メルカトル級数
1668年、ニコラウス・メルカトルによって示された級数です。 $~\log{2}~$ の値が単純な分数の足し算・引き算によって表されます。今回もこの級数を使って、近似値計算... -

ロルの定理は当たり前?定理の意味と証明をわかりやすく解説!
平均値の定理を証明する上で必要なロルの定理。数学の定理ではよくあることですが、書いてあることは当たり前のことでも、数式にするとわかりづらい内容となっています。この記事では、ロルの定理の意味を例示で説明するとともに、ロルの定理の証明を解説!ロルの定理が使えないパターンも示してあるため、定理の中身をしっかりと理解できます。 -

iのi乗
虚数 $~i~$ の $~i~$ 乗はなんと実数になります。実際に $~i^i~$ を計算し、近似値を算出しました。 Ⅰ $~i^i~$ の計算 Ⅱ $~i^i~$ の近似値 【】 $~i~$ の $~i~$ 乗 ... -

複素数の対数関数
対数と言えば $~\log{x}~$ ですが、この定義域を複素数の範囲まで拡張すると、話が単純ではなくなってしまいます。対数関数の表し方とその導き方を紹介します。 Ⅰ 対数... -

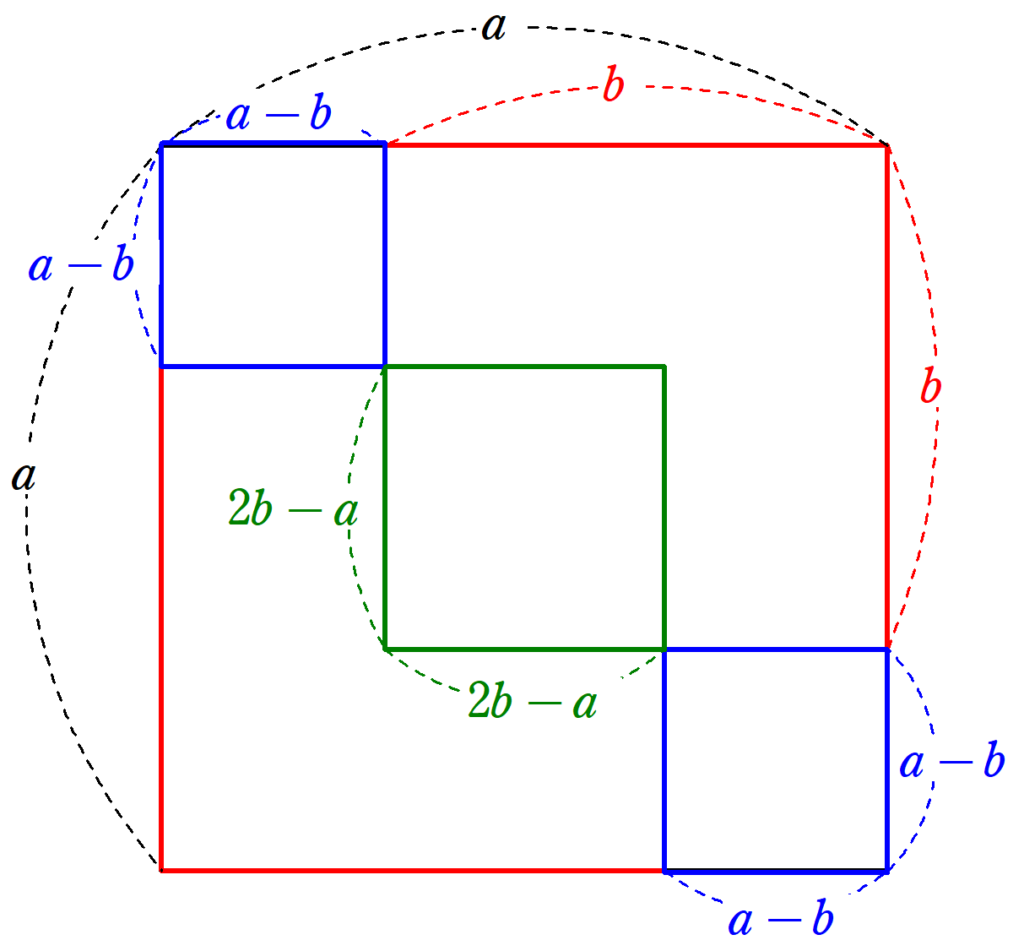
三平方の定理の証明②~ユークリッドの証明方法をわかりやすく解説! 100種類の証明が生まれたのは『原論』が原因?~
三平方の定理の証明ブームを引き起こした張本人ユークリッド。証明ブームの要因となる歴史的著作にも触れつつ、彼自身が考えた三平方の定理の証明について解説します。この記事を読むことで、最も有名な図を使った証明方法を理解できます、 -

三平方の定理の証明①~ピタゴラスの証明の方法をわかりやすく解説! 定理の本当の発見者はバビロニア人?~
この記事では、数ある三平方の定理の証明の中でも、ピタゴラスが証明した方法を現役数学教員が解説します。また、三平方の定理の生みの親はピタゴラスではなかったという歴史にも触れるため、古代ギリシャの時代背景についても理解を深めることができます。 -

【プログラムあり】コラッツ予想を自動計算してみよう!
コラッツ予想とは、単純な定義の計算を繰り返すとどんな自然数も1にたどり着くというもので、未解決問題の1つです。 この記事では、コラッツ予想の紹介をした後、... -

【有名問題】√2が無理数であることの証明~3種類の証明方法とは?~
古代ギリシャから考えられていたルート2 が無理数であることの証明。その歴史の深さと、実際の証明方法を3種類解説します。 -

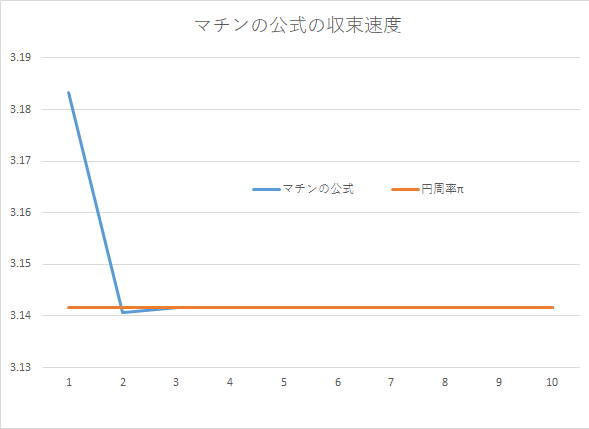
マチンの公式
1706年、イギリスのジョン・マチンによって示された公式です。非常に収束速度が速い級数が使われていて、円周率の $~\displaystyle \frac{1}{4}~$ の値を求めることがで... -

グレゴリー級数
1671年、スコットランドのジェームス・グレゴリーが発見した $~\tan^{-1}x~$ に関する級数です。この級数によって、円周率の近似値の研究が格段に進みました。グレゴリ...