【数学史３－２】バビロニアの数字は2種類だけ！ 60進法の位取りで大きな数も表せる！

　60進法で有名なバビロニア（メソポタミア）。
　この地で使われた楔型文字には、数字も用意されていました。

　その数字は$~10~$と$~1~$のたった２種類。
　どんなに大きな数も、この2つの数字だけで表すことができます。

　それを可能にしたのが、60進法を適用した位取りの考え方。

　この記事では、バビロニアにおける数の表し方を解説します。

時代	B.C.1750年頃
場所	バビロニア（メソポタミア）

バビロニアの数の表し方

　B.C.1750年頃のハンムラビ王の時代には、バビロニアの数体系は確立していました。

　当時の数の表し方を見てみましょう。

楔形文字の数字は2種類のみ

　バビロニア、すなわちメソポタミアでは、楔形の長短の線を組み合わせた楔形文字が発達しました。

　数字についても同様で、楔形の2文字のみが用意されています。

　この2文字を必要な数だけ並べることで、$~1~$から$~59~$までの自然数を表すことができました。

　なぜメソポタミアのことをバビロニアと言うのかは、以下の記事をご覧ください。

60で位が1つ上がる「60進法」

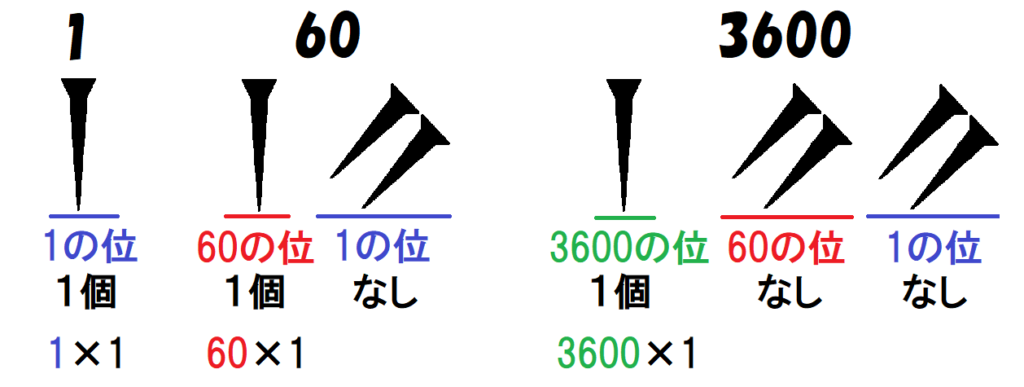
　$~60~$を表す際には、「10」を6個並べることをせず、「1」を60の位に書くことで表します。

　そのため、$~60~$を超える数については、以下のように表すことができました。

　このように、各位に必要な数だけ「10」と「1」の楔形文字を並べることで、$~60~$以上の数も表せます。

「位取り記数法」で大きい数も表せる

　この$~60~$の位、$~1~$の位という考え方は、現代の我々が当たり前のように使っている「位取り記数法」というものです。

　「1234」という数の並びを見たとき、「一二三四」ではなく、「千二百三十四」と読みます。

　これは、「10進法」という位取り記数法を利用していて、右から「1$~(10^0)$の位」、「10$~(10^1)$の位」、「100$~(10^2)$の位」、「1000$~(10^3)$の位」、‥‥と続くことに慣れているからです。

　バビロニアでは、この位取り記数法を「60進法」で行っていて、右から「1$~(60^0)$の位」、「60$~(60^1)$の位」、「3600$~(60^2)$の位」、「216000$~(60^3)$の位」、‥‥と続きます。

　そのため、バビロニアで「1234」と書かれれば、＜図７＞のように解釈され、$~219661~$を表していることになります。

　表している数がいくつなのかをすぐに理解することは難しいものの、２種の文字だけで、いくらでも大きな数を表せるのが、この記数法の利点です。

　古代エジプトでは、この考え方が無かったため、表せる最大の数は$~9999999~$でした。

バビロニアの「位取り記数法」の問題点

　表せる数に際限が無く、便利に見えるバビロニアの「位取り記数法」。

　「60進法」ゆえ、現代の我々からしたら数が読み取りづらいものの、当時のバビロニアでは60進法に慣れていたため、大きな問題ではなかったと考えられます。

　しかし、当時のバビロニアの人たちにとっては、別の大きな問題点がありました。

1と60の区別がつかない

　当時のバビロニアの人たちが抱えていた大きな問題点は、数が読み取れないということ。

　なぜなら、$~0~$を表す文字が無かったからです。

　そのため、「1」という数字が書かれていても、それが$~1~$の位なのか、 $~60~$の位なのか、はたまたそれ以上の位なのかが判別できないのです。

　今の数字においても、$~0~$のおかげで$~1~$（一）、$~10~$（十）、$~100~$（百）を判別できるものの、もし$~0~$が無かったら、全て$~1~$になってしまいます。

数の大きさは文脈から判断していた

　では、バビロニアの人たちがどのように数を判別していたかというと、文脈に依存していました。

　例えば、図8のような文があったとします。

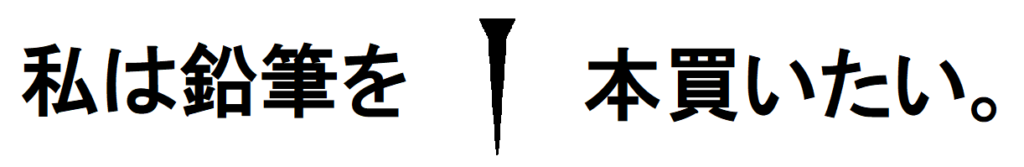
　この文章を見たときに、「1」が$~1~$の位の数字と判断するか、$~60~$の位と判断するか、それ以上の位と判断するかは読者の感覚に委ねられました。

　多くの人は$~1~$本と読むかと思いますが、実際は$~60~$本や$~3600~$本と読んでも間違いではありません。

ペルシャの支配下でゼロ記号が誕生

　紀元前500年頃に、メソポタミア地域がペルシャの支配下となるまで、数を読むことに不自由さを抱えたままでした。

　紀元前3世紀頃になり、楔形文字において位の空所を表す記号が発明されたため、$~1~$と$~60~$と$~3600~$の区別がつくようになっています。

まとめ・参考文献

　バビロニアで使われた数字とそれによる数の表し方について解説しました。

• 楔形文字の数字は「1」と「10」の2種類だけ。
• $~60~$進法により、どんなに大きな数でも表すことができた。
• $~0~$を表す記号が無いため、$~1~$と$~60~$の違いがわからない。

　バビロニアでは、$~1~$よりも細かい数を小数によって表していたため、その説明を次の記事で行います。