【数学史まとめ３】バビロニアの数学

　四大文明の１つとして有名なメソポタミア文明。

　メソポタミアの中にあるバビロンという都市を中心に、栄えた地域をバビロニアと言い、紀元前1750年頃には数体系が確立しました。

　そのため、数学史上では「メソポタミアの数学」を「バビロニアの数学」と言い表しています。

　この記事では、そのバビロニアの数学が発展していく様子を年表形式でまとめるとともに、その内容を解説。

　メソポタミア文明から始まったバビロニアの数学を１つ１つ見ていきましょう。

バビロニアの数学史年表

　数学史上、バビロニアとメソポタミアはほぼ同義です。

　その理由は、紀元前1750年頃のハンムラビ王朝にあります。

　バビロニアの書記たちは、測量などの実用的な部分だけにとどまらず、趣味として数学を研究したため、古代エジプトよりも高度な内容を扱っていました。

バビロニアの数学の内容

　バビロニアでは、粘土板に楔形文字を刻むことで、長期にわたって文字を保存しました。

　古代エジプトのパピルスよりも丈夫であったため、たくさんの資料が現代にまで残っています。

あわせて読みたい

【数学史３－１】メソポタミアとバビロニアの違いは？バビロンって何？歴史から解説！ 四大文明の一つであるメソポタミア文明。数学史上では、メソポタミアの数学は、「バビロニアの数学」と言い表します。しかしながら、バビロニアとメソポタミアって何が違うのでしょうか？また、バビロニアと似たような言葉であるバビロンは何を指すのでしょうか？これらの言葉の違いを、歴史から解説したうえで、メソポタミアの数学がバビロニアの数学となっている経緯を探ります。

数字は2種類のみで60進法を採用

　メソポタミア文明では、紀元前4000年頃から「楔型文字」を使用しています。

　古代エジプトの数字が７種類だったのに対し、楔形文字ではたったの２種類しかありません。

　この２種類の数字を並べることで、$~59~$までの整数は単純に表すことができました。

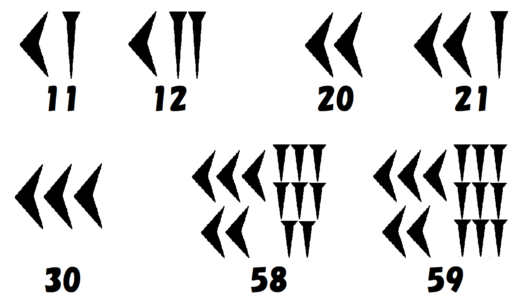
　メソポタミア文明では、$~60~$進法が採用されていたため、$~60~$で位が１つ上がります。

　この世界初の位取り記数法の考え方により、たった２種類の文字だけでどんなに大きな数でも表せるようになりました。

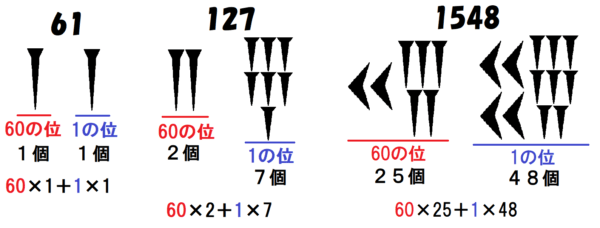
　ただ、$~0~$を表す記号が無かったため、その数字が 1の位なのか 60 の位なのか、はたまた 3600の位なのかが分かりづらいという難点もありました。

あわせて読みたい

【数学史３－２】バビロニアの数字は2種類だけ！ 60進法の位取りで大きな数も表せる！ バビロニア（メソポタミア）では、楔形文字を粘土板に刻むことで、情報を記録していました。土地の借用書や軍備の管理で使われていた粘土板では、数字が必要不可欠であり、２種類の数字が用意されています。この数字と60進法の位取り記数法により、どんな大きな数でも表すことができました。この記事では、その表し方と当時直面した問題点について解説します。

小数も60進法で表した

　古代エジプトが単位分数を好んだのに対し、メソポタミア文明では$~60~$進法による小数が使われました。

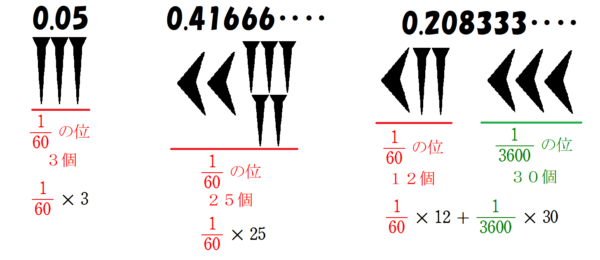
　ただし、小数点や$~0~$という概念が無かったため、小数第何位かがわからないだけでなく、整数と小数の境目すらわからず、前後の文脈から数の大きさを判断するしかありませんでした。

　図７のように「１１」が並んでいたとしても、60の位と1の位で見るか、1の位と小数第１位で見るかは、読んだ人の勝手ということになります。

あわせて読みたい

【数学史３－３】バビロニアでは小数まで60進法！その利点と問題点は？ 2種類の楔形文字で表されるバビロニアの数字。実は、同じ楔形文字で小数も表すことができます。その表し方や問題点、そもそもなぜ60進法がこの地で好まれたのかを、この記事では解説します。

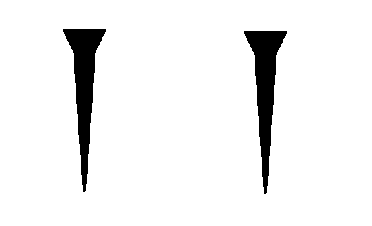
乗除は数表から探すだけ

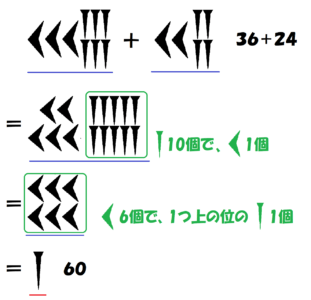
　たし算・ひき算の方法は現在のやり方とほぼ変わりません。

　$~10~$で繰り上がり・繰り下がりをする代わりに、$~60~$でそれを行うという違いだけです。

　しかし、かけ算やわり算は数表を使って行われました。

　かけ算のときに使われた積表は表９のようなもので、かけられる数に関しては40種類の数が用意されていました。

　わり算のときには、積表に加えて逆数表も必要でした。

　逆数表でかけ算に直し、その後積表を使って計算をするという流れでわり算をしていました。

　逆数表は小数点のない数字の羅列だったため、当時のバビロニア人は位取りによる計算ミスが多かったことも粘土板からわかっています。

あわせて読みたい

【数学史３－４】バビロニアの計算方法は？表を見るだけでかけ算とわり算ができる！ 60進法が使われたバビロニアにおいて、かけ算やわり算は「数表」という道具を使って計算しています。かけ算では「積表」を使って調べるだけ、わり算では「逆数表」と「積表」を併用することで答えを出していました。この記事では、その数表の中身や使い方を解説。当時のバビロニア人がわり算で計算ミスをしまくっていた理由もわかります。

「仮置法」で連立方程式を解いた

　未知数が$~x~$のみの一次方程式については、現在と同様、移項などの等式変形を使って解いていたと思われ、バビロニア人にとっては解けて当たり前の問題となっていました。

　粘土板に詳しく解説されていたのは、$~x~$と$~y~$の連立方程式の解き方についてです。

\begin{cases}
&\displaystyle \frac{2}{3}x-\frac{1}{2}y=500~~~\cdots ① \\
&x+y=1800~~~\cdots ②
\end{cases}

\frac{2}{3}\cdot 900-\frac{1}{2}\cdot 900=150

\frac{2}{3}\cdot 1+\frac{1}{2}\cdot 1=\frac{7}{6}

350 \div \frac{7}{6}=300

\begin{cases}&x=900+300=1200 \\&y=900-300=600\end{cases}

　このように、古代エジプトの仮置法のような方法で、連立方程式を華麗に解くことができました。

あわせて読みたい

【数学史３－５】バビロニアでは方程式は当たり前？連立方程式の独特な解法とは？ バビロニアでは、一元一次方程式は当たり前、2文字の連立方程式も様々な方法で解かれていました。現代の数学でも学ぶ「加減法」はもとより、xとyにあてはまる解を仮定してから調整する解き方も開発されており、古代エジプトを凌ぐ代数力を誇っていたことがわかっています。この記事では、そのバビロニアの方程式の解き方について解説します。

二次方程式は3つのパターンに分類

　当時は$~0~$や負の数が無かったため、二次方程式は以下の3つのパターンに分けられました。

 \begin{cases}
 (1)~&x^2-px-q=0  \\
 (2)~&x^2+px-q=0 ~~~~~~~(p,q~は正の定数)  \\
 (3)~&x^2-px+q=0
 \end{cases}

　$(1)$のパターンであれば、以下のような式変形によって、解を導いています。

1. $~p~$の半分をとり、$~\displaystyle \frac{p}{2}~$
2. $~\displaystyle \frac{p}{2}~$に$~\displaystyle \frac{p}{2}~$をかけて、$~\displaystyle \frac{p^2}{4}~$
3. これに$~q~$をたすと、$~\displaystyle \frac{p^2}{4}+q~$
4. これは、$~\displaystyle \sqrt{\frac{p^2}{4}+q}~$の平方
5. ここで、$~\displaystyle \frac{p}{2}~$を$~\displaystyle \sqrt{\frac{p^2}{4}+q}~$をにたして、$~\displaystyle \sqrt{\frac{p^2}{4}+q}+\frac{p}{2}$

　最後に出てくる式を見ると、二次方程式の解の公式と同じ形をしていることがわかります。

　ただし、負の解が出ないように$~\sqrt{}~$の符号は$~\pm~$ではなく、$~+~$限定です。

あわせて読みたい

【数学史３－６】紀元前に二次方程式？バビロニアには解の公式が存在！ バビロニアでは、二次方程式 x²+px+q=0 を、p と q の符号によって場合分けしたうえで、それぞれ独自の方法で解いていました。しかも、それらの方法は「解の公式」や「解と係数の関係」に基づいています。バビロニアの粘土板に載っている、各場合における解き方を紹介すると同時に、それらの解き方が「解の公式」や「解と係数の関係」に繋がっている理由を解説します。

ピタゴラス数の研究が細かい

　バビロニアでは、ピタゴラス数について研究されました。

　そのことが、紀元前1800年頃に書かれたと推定される粘土板プリンプトン322からわかります。

　プリンプトン322は、$~a^2+b^2=c^2~$を満たす数の組$~(a,b,c)~$の値の数表となっています。

　長さが$~c~$と$~a~$の辺のなす角を$~\theta~$とすると、プリンプトン322の数表は$~\theta~$の値が等差数列的に減少していることが窺えます。

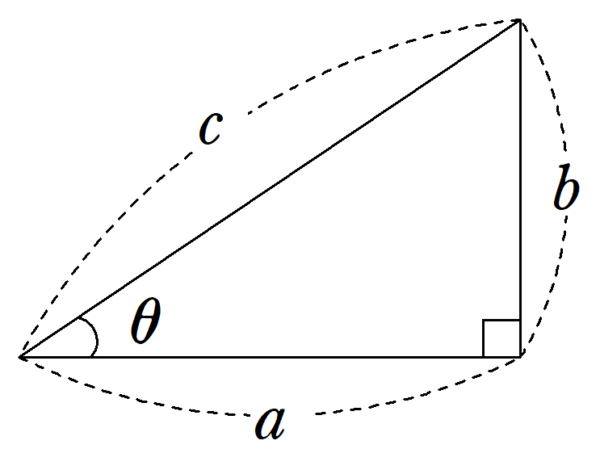
　このことから、バビロニア人は単にピタゴラス数の研究をしていただけでなく、三平方の定理を意識していたことがわかります。

　ピタゴラス（Pythagoras, B.C.569頃-B.C.500頃）が生まれる1000年以上前から、定理自体は知られていた証拠と言えるでしょう。

あわせて読みたい

【数学史３－７】ピタゴラスの定理はバビロニアが最初？粘土板の表に隠された秘密とは？ 紀元前1800年頃のバビロニアでは、すでに三平方の定理が知られていました。ピタゴラスの誕生が紀元前6世紀なので、彼の1000年以上前に研究されていたことになります。その根拠となる粘土板や、そこに書かれていたピタゴラス数の求め方について、この記事では解説します。

相加相乗平均を使って√ の近似値を求めた

　三平方の定理や二次方程式で避けられないのが、平方根。

　粘土板YBC7289では、$~30\sqrt{2}~$の値を見ることができます。

　実際、$~\sqrt{2}~$の近似値は以下のように求めました。

\frac{2}{a_1} < \sqrt{2} < a_1 

a_2=\frac{1}{2}\left(a_1+\frac{2}{a_1} \right)=\frac{1}{2}\left( \frac{3}{2}+\frac{4}{3} \right)=\frac{17}{12}

\begin{align*}a_3&=\frac{1}{2}\left(a_2+\frac{2}{a_2} \right) \\
\\
a_4&=\frac{1}{2}\left(a_3+\frac{2}{a_3} \right) \\
\end{align*}

　この方法で、

\sqrt{2}=1.41421296\cdots

という値を導きました。

まとめ

　メソポタミア文明の数学、すなわちバビロニアの数学について概説してきました。

• 研究好きな書記たちが、数学を実用的な範囲外まで発展させた。
• 60進法でありながら、数表を使って多様な計算を行っていた。
• 二次方程式や三平方の定理といった高度な内容まで扱っていた。

　いろいろな種類の数表を武器に、バビロニア人は実生活の範囲を超えて数学を発展させました。

　バビロニアの書記たちは、それ以後の数学に、抽象的な考え方をする学問という性質を持たせたと言えるでしょう。

次章のまとめへ

【数学史まとめ４】古代インドの数学 四大文明の1つとして有名なインダス文明を起源とする古代インド。インダス文字の解読が進んでいないため、現在わかっている最古のインド数学は、紀元前1000年頃の儀式書『シュルバスートラ』を読み解いたものとなっています。この記事では、古代インド数学の発展に関する出来事を年表形式でまとめるとともに、その内容をざっくり解説します。

解の公式ってこんな昔からあったんだ～。

負の数がないから、場合分けをしているところがすごいよね。