【数学史まとめ４】古代インドの数学

　四大文明の1つとして有名なインダス文明を起源とする古代インド。

　インダス文字の解読が進んでいないため、現在わかっている最古のインド数学は、紀元前1000年頃の儀式書『シュルバスートラ』を読み解いたものとなっています。

　この記事では、古代インド数学の発展に関する出来事を年表形式でまとめるとともに、その内容をざっくり解説。

　実は、現在我々が使っているアラビア数字の祖先もこの時代に生まれました。

時代	B.C.2600年頃～B.C.330年頃
場所	インド

古代インドの数学史年表

　歴史としては、エジプトやバビロニアと同じくらい古いものの、数学に関する史料の登場は一足遅れています。

　インダス文字が解読されていない現在、わかっている範囲で最古の情報は紀元前1000年頃の『シュルバスートラ』となっています。

　『シュルバスートラ』は数学書ではないため、エジプトやバビロニアに比べて圧倒的に情報量が少ないのは事実です。

古代インドの数学の内容

　儀式書『シュルバスートラ』が最有力な文献となるほど、古代インドの数学に関する情報は乏しい状況です。

　使われていた数字と儀式で使われた平面幾何について、見ていきましょう。

数字は全部で20種類で合字を利用していた

　古代インド末期である紀元前4世紀頃、ブラーフミー数字が使われていました。

　$~1~,~2~,~3~$のようなアラビア数字の祖先にあたる数字であり、20種類の数字が用意されていました。

　これらの数以外は、特殊な例を除き、これらの数字をかけ算のように合わせることにより、新たな数字（合字）で表しています。（図2の$~400~$であれば、$~100~$と$~4~$を繋げることで表せる）

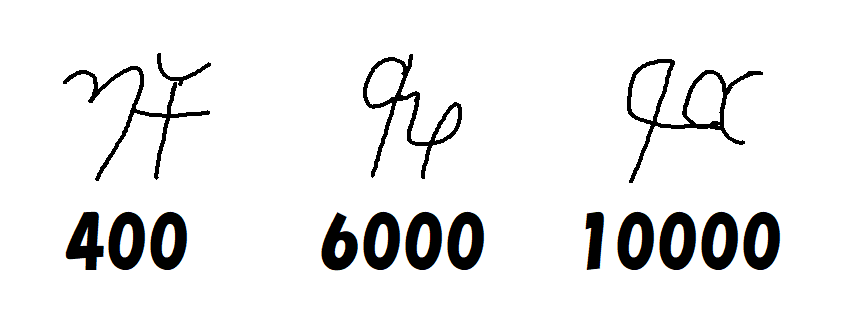
儀式で必要な正方形への作図方法

　『シュルバスートラ』は儀式書のため、祭式で使う図形、すなわち正方形に関する記述が多く残されています。

　例えば、長方形を正方形に等積変形する方法。（図3）

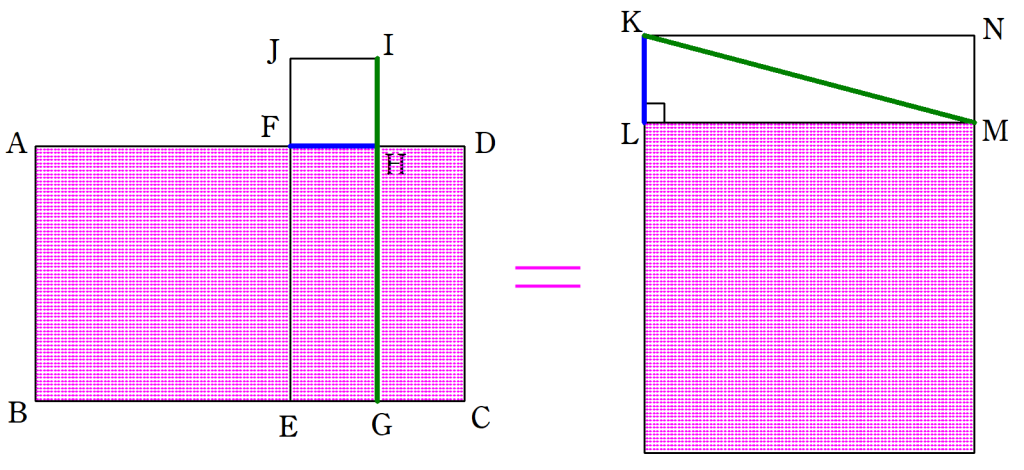
　これにより、正方形を作る際に必要な縄の長さを知ることができました。

　他にも、正方形を2つ足し合わせて、大きな正方形にする方法も載っています。（図4）

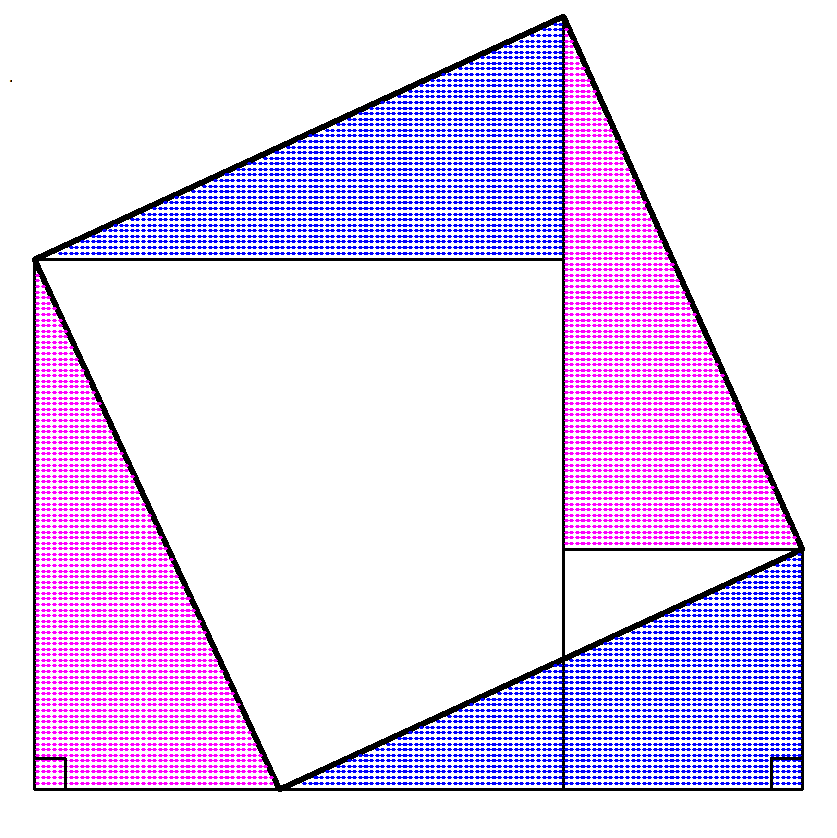
　この図を利用して求めた$~\sqrt{2}~$の値は、小数第5位まで一致していました。

まとめ・参考文献

　古代インドの数学について概説してきました。

• インダス文明の数学は解明されていない。
• 紀元前1000年頃の儀式書『シュルバスートラ』が最古の情報。
• 儀式で縄を張るための等積変形が研究されていた。

　他の四大文明の地に比べ、情報量に欠けるインド数学。

　しかしながら、この記事で紹介した数学こそ、ヨーロッパの影響を受ける以前のインド元来の数学と言えるでしょう。