
毎年8月末に行われる私学適性検査。その解説を作成しました。
解法の一例として、参考にしてください。
- 平成29年度実施の私学適性検査 数学の各問題の解説
他の年度については、コチラからどうぞ。
問題集にも載っていますが、解答だけをまずは示します。
大問1
(1) $~(x-3)(x-2)(x+2)(x+3)~$
(2) $~8192~$
(3) $~\displaystyle \frac{1+\sqrt{5}}{4}~$
(4) $~-512~$
(5) $~30^\circ~$
(6) $~\displaystyle \frac{2\sqrt{19}}{3}~$
(7) 例: $~x=17k+2,y=-28k-3~$ ( $~k~$ は整数)
(8) $~a=4,b=6~$
(9) $~4914~$
(10) $~7.67~$
(11) $~\displaystyle \frac{3}{20}~$
大問2
(1) $~\displaystyle \log{\left| \frac{x-1}{x+2} \right|}+C~$
(2) $~x=-6+2\sqrt{10},y=-6-2\sqrt{10}~$
(3) $~\displaystyle y^{\prime}=x^{e^x}e^x \left( \log{x}+\frac{1}{x} \right)~$
(4) $~0 < a < 80~$
(5) $~\displaystyle \frac{\sqrt{5}}{2}~$
(6) $~\displaystyle \frac{64}{81}~$
(7) 最小値: $~5~$ 、 $~x~$ の値: $~1~$
(8) $~(a,b)=(8,8),(2,-4)~$
(9) $~\log{5}~$
(10) $~k=\displaystyle \frac{5}{2}~$ のとき、共通解は $~2~$ 、
$~k=\displaystyle -\frac{1}{2}~$ のとき、共通解は $~\displaystyle \frac{-1 \pm \sqrt{15}i}{4}~$
大問3
(1) $~S=2~$
(2) $~V_{x}=\displaystyle \frac{1}{2}\pi^2~$
(3) $~V_{y}=2\pi^2~$
大問5
(1) $~\displaystyle \theta=\frac{\pi}{12}~$
(2) $~a=2~$
(3) $~\displaystyle \sin{\theta}=\frac{\sqrt{6}-\sqrt{2}}{4}~,~\cos{\theta}=\frac{\sqrt{6}+\sqrt{2}}{4}~$
大問1
大問1 (1)
$~x^2+x=A~$ と置き換えると、
\begin{align*}
(与式)&=(A-3)(A-15)+27 \\
&=A^2-18A+45+27 \\
&=A^2-18A+72 \\
&=(A-12)(A-6) \\
&=(x^2+x-12)(x^2+x-6) \\
&=(x+4)(x-3)(x+3)(x-2) \\
\end{align*}上式でも正解にはなるが、各カッコ内の定数項を小さい順に並べると、
(x-3)(x-2)(x+3)(x+4)
大問1 (2)
二項定理
(a+b)^n=\sum_{k=0}^{n} {}_n\mathrm{C}_k \cdot a^k \cdot b^{n-k}に、 $~a=1,b=1~$ を代入すると、
(1+1)^n=\sum_{k=0}^{n} {}_n\mathrm{C}_k \cdot 1^k \cdot 1^{n-k}であるため、整理すると、
2^n=\sum_{k=0}^{n} {}_n\mathrm{C}_k ~~~\cdots ①となる。
与式は、①の右辺に $~n=13~$ を代入したものなので、
\begin{align*}
\sum_{k=0}^{13} {}_{13}\mathrm{C}_k&=2^{13} \\
&=8192
\end{align*}大問1 (3)
$~AB=AC=1~,~\angle{A}=36^{\circ}~$の$~\triangle ABC~$を考える。
$~\angle{B}~$の二等分線と$~AC~$の交点を$~D~$とする。
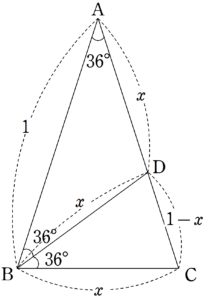

$~BC=x~$とすると、図1のように他の辺も$~x~$を使って表すことができ、$~\triangle ABC~$∽$~ \triangle BCD~$より、
\begin{align*}
1:x&=x:(1-x) \\
x^2&=1-x \\
x^2+x-1&=0 \\
x&=\frac{-1 \pm \sqrt{5}}{2}
\end{align*}で、$~x > 0~$より、$~x=\displaystyle \frac{-1 + \sqrt{5}}{2}~$が求まる。
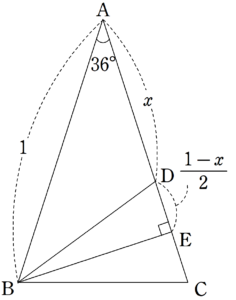

図2のように、$~B~$から$~AC~$におろした垂線の足を$~E~$とすると、$~\triangle ABE~$に注目することで、
\begin{align*}
\cos{36^{\circ}}&=\frac{AE}{1} \\
\\
&=AE \\
\\
&=\displaystyle x+\frac{1-x}{2} \\
\\
&=\frac{x}{2}+\frac{1}{2} \\
\\
&=\frac{-1 \pm \sqrt{5}}{4}+\frac{1}{2} \\
\\
&=\frac{1+ \sqrt{5}}{4}
\end{align*}となる。

大問1 (4)
以下のようにド・モアブルの定理を使って計算していく。
\begin{align*}
&(1+\sqrt{3}i)^9 \\
&=\displaystyle \left\{ 2\left( \frac{1}{2}+\frac{\sqrt{3}}{2}i \right) \right\}^9 \\
\\
&=\left\{ 2\left( \cos{\frac{\pi}{3}}+i\sin{\frac{\pi}{3}} \right) \right\}^9 \\
\\
&=512 \left( \cos{\frac{\pi}{3}}+i\sin{\frac{\pi}{3}} \right)^9 \\
\\
&=512(\cos{3\pi}+i\sin{3\pi}) \\
\\
&=512\cdot (-1) \\
\\
&=-512
\end{align*}大問1 (5)
|\vec{a}||\vec{b}|\cos{\theta}=\vec{a}\cdot \vec{b}より、
\begin{align*}
4\cdot 6 \cdot \cos{\theta}&=12\sqrt{3} \\
\cos{\theta}&=\frac{1}{2}\sqrt{3} \\
\theta&=30^{\circ}
\end{align*}大問1 (6)
2次関数$~y=-3x^2-4x+5~$のグラフと、$~x~$軸の交点の$~x~$座標を$~\alpha~,\beta~(\alpha < \beta )~$とする。
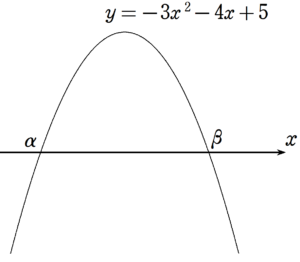

$~-3x^2-4x+5=0~$ で、解と係数の関係から、
\alpha+\beta=-\frac{4}{3}~~,~~\alpha \beta=-\frac{5}{3}となる。
2次関数のグラフが、$~x~$軸から切り取る線分の長さは$~\beta-\alpha~$と表せるので、
\begin{align*}
(\beta-\alpha)^2&=\beta^2-2\alpha\beta+\alpha^2 \\
&=(\alpha+\beta)^2-4\alpha\beta \\
\\
&=\left( -\frac{4}{3} \right)^2 - 4 \cdot \left( -\frac{5}{3} \right) \\
\\
&=\frac{16}{9}+\frac{20}{3} \\
\\
&=\frac{76}{9}
\end{align*}となる。
両辺正の平方根をとることで、
\beta-\alpha=\frac{2\sqrt{19}}{3}大問1 (7)
28\cdot 2+17 \cdot (-3)=5 \cdots②
より、特殊解は $~x=2,y=-3~$ である。
元の式から$②$を引き、式変形していくと、
\begin{align*}
28(x-2)+17(y+3)&=0 \\
28(x-2)&=-17(y+3) ~~~\cdots③ \\
\end{align*}となる。
$~28~$ と $~17~$ は互いに素なので、$k~$を整数として、
x-2=17k ~~~ \cdots④
であるため、$~x=17k+2~$と表せる。
また、$④$を$③$に代入すると、
\begin{align*}
28 \cdot 17k&=-17(y+3) \\
28k&=-(y+3) \\
-28k&=y+3 \\
-28k-3&=y
\end{align*}となるため、以上より、
x=17k+2~,~y=-28k-3~~~~~(kは整数)
大問1 (8)
出てくる数式をそれぞれ整理していく。
\begin{align*}
(f \circ g)(x)&=f(g(x)) \\
&=f(ax+b) \\
&=3(ax+b)+4 \\
&=3ax+3b+4 ~~~~\cdots⑤
\end{align*}\begin{align*}
(g \circ f)(x)&=g(f(x)) \\
&=g(3x+4) \\
&=a(3x+4)+b \\
&=3ax+4a+b ~~~~\cdots⑥
\end{align*}\begin{align*}
f(2)&=3\cdot2+4 \\
&=10 ~~~\cdots⑦
\end{align*}g(1)=a+b ~~~~\cdots⑧
$~⑤=⑥~$ より、
3b+4=4a+b ~~~~~\cdots⑨
で、$~⑦=⑧~$ より、
a+b=10 ~~~~\cdots⑩
が成り立つ。
よって、$~⑨~,~⑩~$の連立方程式を解くと、
a=4~,~b=6
大問1 (9)
$~1440~$ を素因数分解すると、
1440=2^5\cdot 3^2\cdot 5
であり、この結果に「約数の総和」を求める式を使うと、
\begin{align*}
&(1+2+2^2+2^3+2^4+2^5)(1+3+3^2)(1+5) \\
&=63 \cdot 13 \cdot 6 \\
&=4914
\end{align*}大問1 (10)
まず、$~a~$を求める。
平均値が $~2a~$であることから、
\begin{align*}
\frac{10+a+12+8+9+5}{6}&=2a \\
44+a&=12a \\
-11a&=-44 \\
a&=4
\end{align*}であり、平均値は $~2 \cdot 4=8~$ 。
分散は、(2乗の平均)-(平均の2乗)で求まるため、(2乗の平均)を求めると、
\begin{align*}
&\frac{100+16+144+64+81+25}{6} \\
\\
&=\frac{430}{6} \\
\\
&=\frac{215}{3} \\
\end{align*}である。
したがって分散は、
\begin{align*}
\displaystyle &\frac{215}{3}-8^2 \\
\\
&=\frac{215}{3}-\frac{192}{3} \\
\\
&=\frac{23}{3} \\
\\
&\fallingdotseq 7.666
\end{align*}であり、小数第2位を四捨五入して、分散は $~7.67~$ 。
大問1 (11)
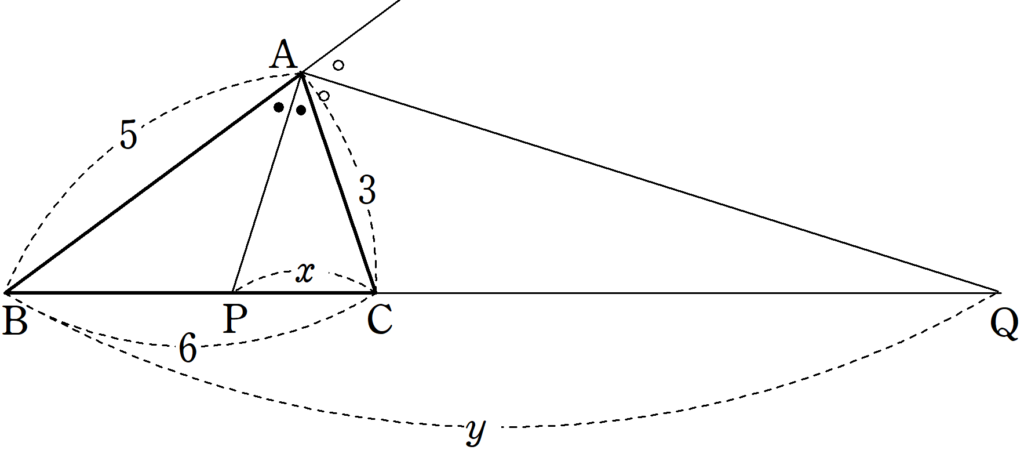

$~PC=x~$ とする。内角二等分線の性質より、
\begin{align*}
5:3&=(6-x):x \\
3(6-x)&=5x \\
18-3x&=5x \\
-8x&=-18 \\
x&=\frac{9}{4}
\end{align*}が求まる。
また、 $~BQ=y~$ とすると、外角二等分線の性質より、
\begin{align*}
3:(y-6)&=5:y \\
5(y-6)&=3y \\
5y-30&=3y \\
2y&=30 \\
y&=15
\end{align*}が求まる。
したがって、
\begin{align*}
\frac{PC}{BQ}&=\frac{\frac{9}{4}}{15} \\
\\
&=\frac{9}{60} \\
\\
&=\frac{3}{20}
\end{align*}である。
大問2
大問2 (1)
\begin{align*}
& \int \frac{3}{x^2+x-2}dx \\
\\
&=3\int \frac{1}{(x-1)(x+2)}dx ~~~~\cdots⑪
\end{align*}ここで、$~\displaystyle \frac{1}{(x-1)(x+2)}~$を部分分数分解することを考える。
\frac{1}{(x-1)(x+2)}=\frac{a}{x-1}+\frac{b}{x+2}~~~\cdots ⑫として、両辺に$~(x-1)(x+2)~$をかけると、
\begin{align*}
1&=a(x+2)+b(x-1) \\
1&=ax+2a+bx-b \\
1&=(a+b)x+(2a-b) \\
\end{align*}となるため、両辺の係数を比較して、
\begin{cases}
a+b=0 & \\
2a-b=1 &
\end{cases}より、$~\displaystyle a=\frac{1}{3}~,~b=-\frac{1}{3}~$がわかる。
よって、$⑫$は、
\begin{align*}
\frac{1}{(x-1)(x+2)}&=\frac{\frac{1}{3}}{x-1}-\frac{\frac{1}{3}}{x+2} \\
\\
&=\frac{1}{3} \left( \frac{1}{x-1}-\frac{1}{x+2} \right)~~~\cdots ⑬
\end{align*}と部分分数分解できた。
$⑬$を$⑪$に代入して、
\begin{align*}
&3\int \frac{1}{3} \left( \frac{1}{x-1}-\frac{1}{x+2} \right) dx \\
\\
&=\int \frac{1}{x-1}-\frac{1}{x+2} dx \\
\\
&=\log{|x-1|}-\log{|x+2|}+C \\
\\
&=\log{\left| \frac{x-1}{x+2} \right|}+C
\end{align*}大問2 (2)
\begin{cases}
x+y-3xy=0 ~~~\cdots⑭ & \\
-x-y+2xy=4 ~~~~\cdots⑮&
\end{cases}とする。
$⑭+⑮$より、
\begin{align*}
-xy&=4 \\
xy&=-4 ~~~\cdots⑯
\end{align*}であり、$⑭\times 2+⑯ \times 3~$ より、
\begin{align*}
-x-y&=12 \\
x+y&=-12 ~~~\cdots ⑰
\end{align*}となる。
$⑯~,~⑰$より、2次方程式の解と係数の関係から、$~~$の解$~t~$が $~x~,~y~$であることがわかる。
この$~t~$の2次方程式を解くと、
\begin{align*}
t^2+12t-4&=0 \\
t&=-6 \pm \sqrt{40} \\
t&=-6 \pm 2\sqrt{10}
\end{align*}$~x \ge y ~$より、$~x=-6+2\sqrt{10}~,~y=-6-2\sqrt{10}~$が求まった。
大問2 (3)
$~x > 0~$より、$~x^{e^x} > 0~$である。
$~y=x^{e^x}~$において、両辺自然対数をとると、
\begin{align*}
\log{y}&=\log{x^{e^x}} \\
\log{y}&=e^x \log{x} \\
\end{align*}となる。
この両辺を $~x~$ で微分すると、
\begin{align*}
\frac{1}{y}\cdot y'&=(e^x)'\cdot \log{x}+e^x \cdot (\log{x})' \\
\\
\frac{1}{y}\cdot y'&=e^x \log{x}+e^x \cdot \frac{1}{x} \\
\\
y'&=ye^x \left( \log{x}+ \frac{1}{x} \right) \\
\\
y'&=x^{e^x} e^x \left( \log{x}+ \frac{1}{x} \right) \\
\end{align*}大問2 (4)
f(x)=x^3-3x^2-24x+a
として、この$~f(x)~$を$~x~$で微分すると、
f'(x)=3x^2-6x-24
となる。
$~f'(x)=0~$となる$~x~$を求めると、
\begin{align*}
3x^2-6x-24&=0 \\
x^2-2x-8&=0 \\
(x+2)(x-4)&=0 \\
x&=-2,4
\end{align*}であるため、$~f(x)~$の増減表は図5のように書ける。
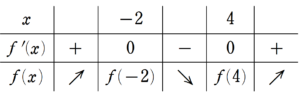
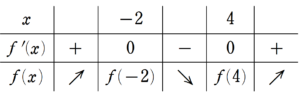
この増減表から、$~f(0)=0~$が正の解を2個、負の解を1個持つように$~y=f(x)~$のグラフを書くと、図6のようになる。
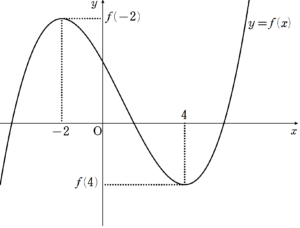

図6のグラフから、満たすべき条件式は
\begin{cases}
f(-2) > 0 & \\
f(0) > 0 & \\
f(4) < 0 &
\end{cases} であり、これらの不等式を解くと、
\begin{cases}
a > -28 & \\
a > 0 & \\
a < 80 & \end{cases} となる。
以上の解の共通範囲をとることで、$~0 < a < 80~$が求まった。
大問2 (5)
$~\triangle ABC~$の三辺の長さがわかっているので、ヘロンの公式を使うと、$~\displaystyle s=\frac{3+7+6}{2}=8~$ として、
\begin{align*}
\triangle ABC&=\sqrt{8\cdot(8-3)\cdot(8-7)\cdot(8-6)} \\
&=\sqrt{8\cdot 5 \cdot 1 \cdot 2} \\
&=4\sqrt{5}
\end{align*}が求まる。
よって、$~\triangle ABC~$の内接円の半径を$~r~$とすると、
\begin{align*}
\frac{1}{2}r(3+7+6)&=4\sqrt{5} \\
\\
8r&=4\sqrt{5} \\
\\
r&=\frac{\sqrt{5}}{2}
\end{align*}が求まる。
大問2 (6)
Aが優勝するパターンは、次の3パターンに分けられる。
\begin{cases}
(\text{i})&~勝+勝+勝 \\
\\
(\text{ii})&~\underbrace{\blacksquare \blacksquare \blacksquare }_{2勝1敗}~+勝 \\
\\
(\text{iii})&~\underbrace{ \blacksquare \blacksquare \blacksquare \blacksquare }_{2勝2敗}~+勝
\end{cases}
(i)のパターン
Aが3試合連続で勝つので、
\left( \frac{2}{3} \right)^3=\frac{8}{27}(ii)のパターン
最初の3試合は反復試行、4試合目はAが勝つので、
\begin{align*}
\left\{ {}_3\mathrm{C}_2 \cdot \left( \frac{2}{3} \right)^2 \cdot \left( \frac{1}{3} \right) \right\} \cdot \frac{2}{3} &=3\cdot \frac{4}{9} \cdot \frac{1}{3} \cdot \frac{2}{3} \\
\\
&=\frac{8}{27}
\end{align*}
(iii)のパターン
最初の4試合は反復試行、5試合目はAが勝つので、
\begin{align*}
\left\{ {}_4\mathrm{C}_2 \cdot \left( \frac{2}{3} \right)^2 \cdot \left( \frac{1}{3} \right)^2 \right\} \cdot \frac{2}{3} &=6\cdot \frac{4}{9} \cdot \frac{1}{9} \cdot \frac{2}{3} \\
\\
&=\frac{16}{81}
\end{align*}
(i)~(iii)より、求めるべき確率は、
\begin{align*}
\frac{8}{27}+\frac{8}{27}+\frac{16}{81}&=\frac{24}{81}+\frac{24}{81}+\frac{16}{81} \\
\\
&=\frac{64}{81}
\end{align*}となる。
大問2 (7)
$~x > -3~$より、$~x+3 > 0~$となるため、相加相乗平均の関係より、
\begin{align*}
(与式)&=\left\{ (x+3)+\frac{16}{x+3} \right\}-3 \\
\\
&\ge 2\sqrt{(x+3)\cdot \frac{16}{x+3}} -3 \\
\\
&=2\sqrt{16}-3 \\
&=2\cdot 4-3 \\
&=5
\end{align*}であるため、最小値は$~5~$となる。
また、最小値をとるのは$~x~$が次の式を満たすときなので、
\begin{align*}
x+3&=\frac{16}{x+3} \\
(x+3)^2&=16 \\
x+3&=\pm 4 \\
x&=-7,1
\end{align*}であり、$~x > -3~$から$~x=1~$が求まる。
大問2 (8)
$~8~,~a~,~b~$の等差数列の公差を$~d~$とすると、
\begin{cases}
a=8+d & \\
b=8+2d &
\end{cases}が成り立ち、この2式から$~d~$を消去すると、
2a-b=8 ~~~\cdots ⑱
である。
次に、$~a~,~b~,~8~$の等比数列の公比を$~r~$とすると、
\begin{cases}
b=ar & \\
8=ar^2 &
\end{cases}が成り立ち、上の式を変形した$~\displaystyle r=\frac{b}{a}~$を、下の式に代入することで、
\begin{align*}
8&=a \left(\frac{b}{a} \right)^2 \\
\\
8&=\frac{b^2}{a} \\
\\
8a&=b^2 ~~~\cdots⑲
\end{align*}となる。
$⑱$を4倍した式に、$⑲$を代入して方程式を解くと、
\begin{align*}
b^2-4b&=32 \\
b^2-4b-32&=0 \\
(b+4)(b-8)&=0 \\
b&=-4,8
\end{align*}で、それぞれ$⑱$に代入すると、
(a,b)=(2,-4),(8,8)
となるものの、$~(a,b)=(8,8)~$のときは、等差数列や等比数列にならないので不適。
大問2 (9)
$~5^x-1=t~$とおく。
このとき、$~x \to 0~$なので、$~t \to 0~$となる。
$~5^x=t+1~$の両辺に、~5~を底とした対数をとると、$~x=\log_{5}{(t+1)}~$であるため、与式に代入すると、
\begin{align*}
(与式)&=\lim_{t \to 0}\frac{t}{\log_5{(t+1)}} \\
\\
&=\lim_{t \to 0}\frac{t}{\frac{\log{(t+1)}}{\log{5}}} \\
\\
&=\lim_{t \to 0}\frac{\log{5}}{\frac{1}{t}\log{(t+1)}} \\
\\
&=\lim_{t \to 0}\frac{\log{5}}{\log{(t+1)^{\frac{1}{t}}}} \\
\\
&=\frac{\log{5}}{\log{e}} \\
\\
&=\log{5}
\end{align*}が求まる。
※ロピタルの定理を使って求めることもできます。
大問2 (10)
2つの二次方程式の共通解を$~\alpha~$とする。それぞれの方程式に代入して、
\begin{cases}
\alpha^2-k\alpha+1=0 ~~~\cdots⑳& \\
2\alpha^2+\alpha-4k=0 ~~~\cdots㉑&
\end{cases}である。
$~⑳\times 2-㉑~$ より、
\begin{align*}
(-2k-1)\alpha+(2+4k)&=0 \\
-(2k+1)\alpha+2(2k+1)&=0 \\
(2k+1)(-\alpha+2)&=0 \\
\end{align*}となるので、$~\displaystyle k=-\frac{1}{2}~$または$~\alpha=2~$である。
$~\displaystyle k=-\frac{1}{2}~$のとき
$⑳$と$㉑$はそれぞれ、
\begin{cases}
\alpha^2+\frac{1}{2}\alpha+1=0 ~~~\cdots⑳'& \\
2\alpha^2+\alpha+2=0 ~~~~\cdots㉑' &
\end{cases}となり、 $~⑳’ \times 2=㉑’~$ であるため、 $~㉑’~$ の方程式で解の公式を使うと、
\begin{align*}
\alpha&=\frac{-1 \pm \sqrt{1-16}}{4} \\
\\
&=\frac{-1 \pm \sqrt{15}i}{4} \\
\end{align*}が求まる。
$~\alpha=2~$ のとき、
$⑳$と$㉑$はそれぞれ、
\begin{cases}
5-2k=0 ~~~\cdots⑳''& \\
10-4k=0 ~~~\cdots㉑''&
\end{cases}となり、 $~⑳” \times 2=㉑”~$ であるため、 $~⑳”~$ の方程式を解くと、
k=\frac{5}{2}が求まる。
以上より、$\displaystyle k=\frac{5}{2}~$のとき、共通解は$~2~$、
$~\displaystyle k=-\frac{1}{2}~$のとき、共通解は$~\displaystyle \frac{-1 \pm \sqrt{15}i}{4}~$が求まった。
大問3
大問3 (1)
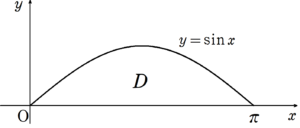

グラフは図7のようになるので、
\begin{align*}
S&=\int_{0}^{\pi} \sin{x}dx \\
\\
&=\left[ -\cos{x} \right]_{0}^{\pi} \\
&=1-(-1) \\
&=2
\end{align*}と求まる。
大問3 (2)
$~x~$軸の周りに1回転してできる立体の体積$~V_x~$は、
V_{x}=\displaystyle \int \pi y^2 dxで求まるので、図7より、
\begin{align*}
V_{x}&=\int_{0}^{\pi} \pi \sin^2{x} dx \\
\\
&=\pi \int_{0}^{\pi}\sin^2{x} dx ~~~~\cdots㉒
\end{align*}となる。
ここで、半角の公式
\sin^2{\frac{x}{2}}=\frac{1-\cos{x}}{2}より、
\sin^2{x}=\frac{1-2\cos{x}}{2} \\を$㉒$に代入して、
\begin{align*}
V_{x}&= \pi \int_{0}^{\pi}\frac{1-\cos{2x}}{2} dx \\
\\
&=\frac{1}{2}\pi \int_{0}^{\pi} 1-\cos{2x} dx \\
\\
&=\frac{1}{2}\pi \left[ x-\frac{1}{2}\sin{2x} \right]_{0}^{\pi} \\
\\
&=\frac{1}{2}\pi \{ \pi \} \\
\\
&=\frac{1}{2}\pi^2
\end{align*}が求まった。
※もちろん$~\displaystyle \int_{0}^{\pi} \pi \sin^2{x} dx=2 \int_{0}^{\frac{\pi}{2}} \pi \sin^2{x} dx~$としても求まります。
大問3 (3)
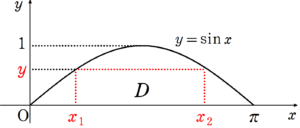

図8より、
\begin{align*}
V_{y}&= \int_{0}^{1} \pi x_{2}^2-\pi x_{1}^2dy \\
\\
&=\pi \int_{0}^{1} x_{2}^2dy - \pi \int_{0}^{1} x_{1}^2dy \\
\end{align*}を求めればよい。
ここで、$~y=\sin{x}~$より、$~\displaystyle \frac{dy}{dx}=\cos{x}~$すなわち、$~dy=\cos{x}dx~$である。
また、$~y: 0 \to 1~$より、$~\displaystyle x_1: 0 \to \frac{\pi}{2}~,~x_2: \pi \to \frac{\pi}{2}~$なので、
V_{y}=\pi \int_{\pi}^{\frac{\pi}{2}} x_{2}^2\cos{x_2}dx_2 - \pi \int_{0}^{\frac{\pi}{2}} x_{1}^2\cos{x_1}dx_1 ~~~\cdots㉓となる。
ここで、それぞれの積分を部分積分(積分定数$~C~$は省略)で考えると、
\begin{align*}
&\int x^2 \cos{x}dx \\
\\
&=x^2 \sin{x}-2\int x \sin{x}dx \\
\\
&=x^2 \sin{x}-2 \left( -x\cos{x}+\int \cos{x}dx \right) \\
\\
&=x^2 \sin{x}+2x\cos{x}-2\int \cos{x}dx \\
\\
&=x^2 \sin{x}+2x\cos{x}-2\sin{x}
\end{align*}となるため、$㉓$に利用して、
\begin{align*}
V_{y}&=\pi \left[ x^2 \sin{x}+2x\cos{x}-2\sin{x}\right]_{\pi}^{\frac{\pi}{2}}-\pi \left[x^2\sin{x}+2x\cos{x}-2\sin{x} \right]_{0}^{\frac{\pi}{2}} \\
\\
&=\pi \left\{ \left( \frac{\pi^2}{4}-2 \right)- \left( -2\pi \right) \right\}-\pi \left\{ \frac{\pi^2}{4}-2 \right\} \\
\\
&=\pi \left( \frac{\pi^2}{4}-2+2\pi \right)-\pi \left( \frac{\pi^2}{4}-2 \right) \\
\\
&=\frac{\pi^3}{4}-2\pi+2\pi^2-\frac{\pi^3}{4}+2\pi \\
\\
&=2\pi^2
\end{align*}が求まった。
大問4
大問4 (1)
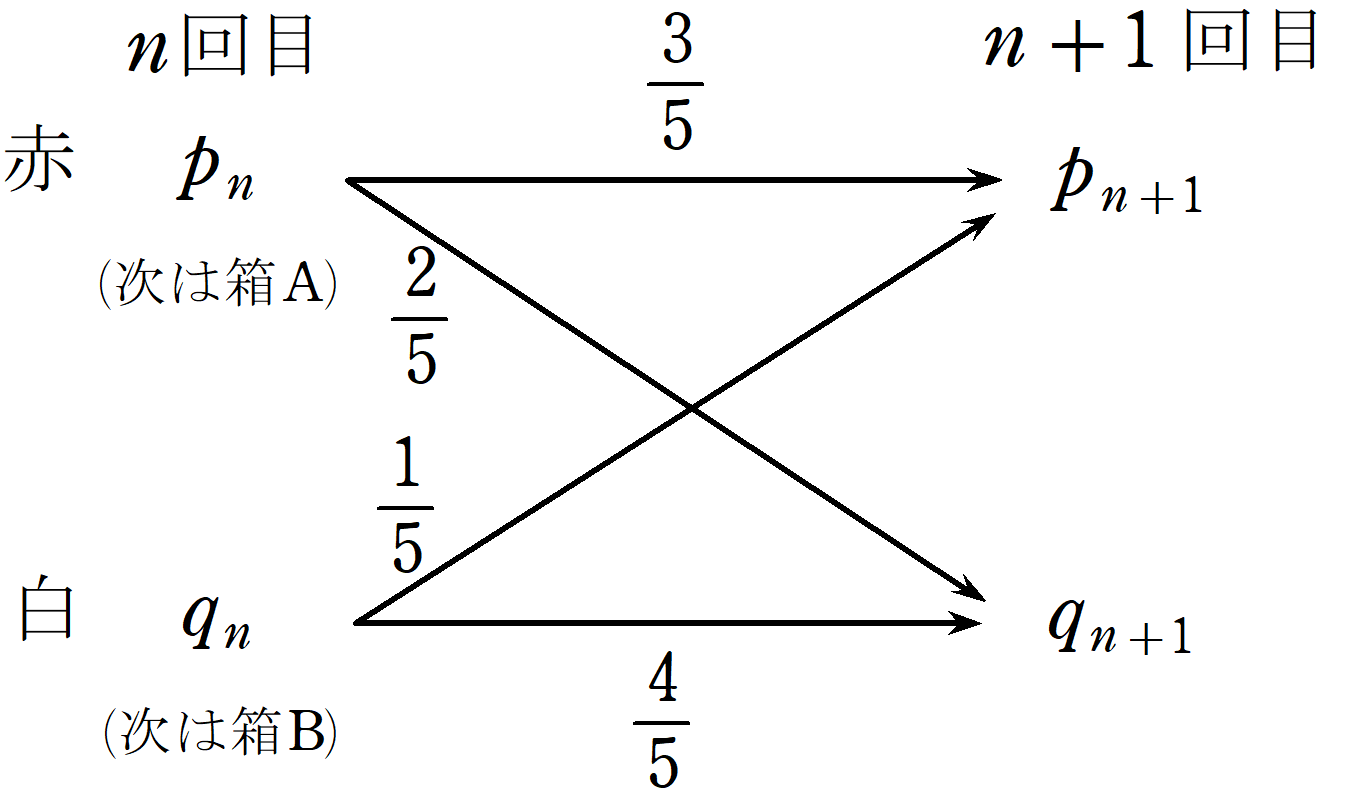
箱Aから赤玉がとられる確率は$~\displaystyle \frac{3}{5}~$、白玉がとられる確率は$~\displaystyle \frac{2}{5}~$である。
箱Bから赤玉がとられる確率は$~\displaystyle \frac{1}{5}~$、白玉がとられる確率は$~\displaystyle \frac{4}{5}~$である。
$~n~$ 回目の試行で赤玉をとった場合、$~n+1~$回目は箱Aから玉をとり、$~n~$回目の試行で白玉をとった場合、 $~n+1~$回目は箱Bから玉をとるため、確率推移は図9のようになる。

この図9をもとに、$~n~$ 回目と$~n+1~$回目の関係を式で表すと、
\begin{cases}
\displaystyle p_{n+1}=\frac{3}{5}p_n+\frac{1}{5}q_n & \cdots㉔ \\
\\
\displaystyle q_{n+1}=\frac{2}{5}p_n+\frac{4}{5}q_n & \cdots㉕
\end{cases}となる。
ここで、 $~p_n+q_{n}=1~$より、$㉔$は、
\begin{align*}
p_{n+1}&=\frac{3}{5}p_n+\frac{1}{5}(1-p_n) \\
\\
p_{n+1}&=\frac{3}{5}p_n+\frac{1}{5}-\frac{1}{5}p_n \\
\\
p_{n+1}&=\frac{2}{5}p_n+\frac{1}{5}~~~\cdots ㉖
\end{align*}となり、$㉕$の式は、
\begin{align*}
q_{n+1}&=\frac{2}{5}(1-q_n)+\frac{4}{5}q_n \\
\\
q_{n+1}&=\frac{2}{5}-\frac{2}{5}q_n+\frac{4}{5}p_n \\
\\
q_{n+1}&=\frac{2}{5}q_n+\frac{2}{5}~~~~\cdots㉗
\end{align*}となる。
大問4 (2)
$㉖$の漸化式を特性方程式を使って、解く。
$~p_{n}~,~p_{n+1}~$を$~x~$とおくと、
\begin{align*}
\displaystyle x&=\frac{2}{5}x+\frac{1}{5} \\
\\
\frac{3}{5}x&=\frac{1}{5} \\
\\
x&=\frac{1}{3}
\end{align*}となるため、$㉖$は、
p_{n+1}-\frac{1}{3}=\frac{2}{5}\left( p_n-\frac{1}{3} \right) と式変形でき、この式は、公比$~\displaystyle \frac{2}{5}~$、初項$~\displaystyle p_1-\frac{1}{3}=\frac{3}{5}-\frac{1}{3}=\frac{4}{15}~$の数列$~\displaystyle \left\{ p_n-\frac{1}{3} \right\}~$を表すので、一般項は
\begin{align*}
p_n-\frac{1}{3}&=\left( \frac{2}{5} \right)^{n-1}\cdot \frac{4}{15} \\
\\
p_n&=\frac{4}{15}\cdot \left( \frac{2}{5} \right)^{n-1}+\frac{1}{3}
\end{align*}と求まる。
また、$㉗$についても同様に特性方程式を使って解いていく。
$~q_{n}~,~q_{n+1}~$を$~y~$とおくと、
\begin{align*}
y&=\frac{2}{5}y+\frac{2}{5} \\
\\
\frac{3}{5}y&=\frac{2}{5}\\
\\
y&=\frac{2}{3}
\end{align*}となるため、$㉗$は
q_{n+1}-\frac{2}{3}=\frac{2}{5}\left( q_n-\frac{2}{3} \right)と式変形でき、この式は、公比$~\displaystyle \frac{2}{5}~$、初項$~\displaystyle q_1-\frac{2}{3}=\frac{2}{5}-\frac{2}{3}=-\frac{4}{15}~$の数列$~\displaystyle \left\{ q_n-\frac{2}{3} \right\}~$を表すので、 一般項は
\begin{align*}
q_n-\frac{2}{3}&=\left( \frac{2}{5} \right)^{n-1}\cdot \left( -\frac{4}{15} \right) \\
\\
q_n&=-\frac{4}{15}\cdot \left( \frac{2}{5} \right)^{n-1}+\frac{2}{3}
\end{align*}と求まった。
大問4 (3)
(2)で求めた$~p_n~,~q_n~$をそれぞれ代入して、$~\displaystyle \lim_{n \to \infty}\left( \frac{2}{5} \right)^{n-1}=0~$であることを考えると、
\begin{align*}
\lim_{n \to \infty}p_n&= \lim_{n \to \infty} \left\{ \frac{4}{15}\cdot \left( \frac{2}{5} \right)^{n-1}+\frac{1}{3}
\right\} \\
\\
&=\frac{4}{15}\cdot 0+\frac{1}{3} \\
\\
&=\frac{1}{3} \\
\\
\lim_{n \to \infty}q_n&=\lim_{n \to \infty}\left\{ -\frac{4}{15}\cdot \left( \frac{2}{5} \right)^{n-1}+\frac{2}{3} \right\} \\
\\
&=-\frac{4}{15}\cdot 0+\frac{2}{3} \\
\\
&=\frac{2}{3}
\end{align*}が求まった。
大問5
大問5 (1)
$~0 < \theta < \displaystyle \frac{\pi}{4}~$より、$~1 > \cos{\theta} > \sin{\theta} > 0 ~$が成り立つため、
1 < \frac{1}{\cos{\theta}} < \frac{1}{\sin{\theta}}~~~~\cdots ㉘が言える。
$~x~$の二次方程式$~x^2-2\sqrt{6}x-a^2+4a=0~$で、解と係数の関係より、
\frac{1}{\cos{\theta}} + \frac{1}{\sin{\theta}}=2\sqrt{6}が成り立つ。
この式の両辺に$~\sin{\theta}\cos{\theta}~$をかけて式変形すると、
\begin{align*}
\sin{\theta}+\cos{\theta}&=2\sqrt{6}\sin{\theta}\cos{\theta} ~~~\cdots ㉙\\
(\sin{\theta}+\cos{\theta})^2&=(2\sqrt{6}\sin{\theta}\cos{\theta})^2 \\
\sin^2{\theta}+2\sin{\theta}\cos{\theta}+\cos^2{\theta}&=24(\sin{\theta}\cos{\theta})^2 \\
1+2\sin{\theta}\cos{\theta}&=24(\sin{\theta}\cos{\theta})^2 \\
\end{align*}であり、ここで$~\sin{\theta}\cos{\theta}=t~$とおくと、
\begin{align*}
1+2t&=24t^2 \\
24t^2-2t-1&=0 \\
(4t-1)(6t+1)&=0 \\
t&=\frac{1}{4}~,~-\frac{1}{6} \\
\end{align*}となるため、$~t=\sin{\theta}\cos{\theta} > 0~$より、
t=\sin{\theta}\cos{\theta}=\frac{1}{4}~~~\cdots ㉚が求まる。
これを$㉙$に代入することで、
\begin{align*}
\displaystyle \sin{\theta}+\cos{\theta}&=2\sqrt{6}\cdot \frac{1}{4} \\
\\
\sqrt{2} \sin{\left(\theta+\frac{\pi}{4} \right)}&=\frac{\sqrt{6}}{2} \\
\\
\sin{\left(\theta+\frac{\pi}{4} \right)}&=\frac{\sqrt{3}}{2} \\
\end{align*}と変形できるので、$~\displaystyle \frac{\pi}{4} < \theta+\frac{\pi}{4} < \frac{\pi}{2}~$より、
\begin{align*}
\theta+\frac{\pi}{4}&=\frac{\pi}{3} \\
\\
\theta&=\frac{\pi}{12}
\end{align*} 大問5 (2)
$~x~$の二次方程式$~x^2-2\sqrt{6}x-a^2+4a=0~$で、解と係数の関係より、
\frac{1}{\cos{\theta}}\cdot \frac{1}{\sin{\theta}}=-a^2+4aが成り立ち、$㉚$を代入することで、
\begin{align*}
\frac{1}{\frac{1}{4}}&=-a^2+4a \\
\\
4&=-a^2+4a \\
a^2-4a+4&=0 \\
(a-2)^2&=0 \\
a&=2
\end{align*}が求まった。
大門5 (3)
元の二次方程式に$~a=2~$を代入すると、
x^2-2\sqrt{6}+4=0であり、この二次方程式を解の公式で解くと、
x=\sqrt{6} \pm \sqrt{2}が求まる。
$㉘$より、
\frac{1}{\cos{\theta}}=\sqrt{6} - \sqrt{2}~~,~~\frac{1}{\sin{\theta}}= \sqrt{6} + \sqrt{2}と定まる。
よって、
\cos{\theta}=\frac{1}{\sqrt{6} - \sqrt{2}}~~,~~\sin{\theta}= \frac{1}{\sqrt{6} + \sqrt{2}}であり、それぞれ有理化することで、
\begin{align*}
\cos{\theta}&=\frac{\sqrt{6}+\sqrt{2}}{(\sqrt{6}-\sqrt{2})(\sqrt{6}+\sqrt{2})} \\
\\
&=\frac{\sqrt{6} + \sqrt{2}}{4} \\
\\
\sin{\theta}&=\frac{\sqrt{6}-\sqrt{2}}{(\sqrt{6}+\sqrt{2})(\sqrt{6}-\sqrt{2})} \\
\\
&=\frac{\sqrt{6} - \sqrt{2}}{4} \\
\end{align*}が求まった。



地味に\cos{36^{\circ}}の値って難しいよね。



黄金比に気付けた人は解けるけど、それでも計算量がすごい‥‥。
限られた時間の中でどれだけ解けるかが勝負です。
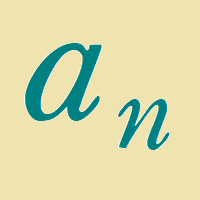
コメント