円の面積をどのように求めるか？
現在では円周率3.14を用いて計算しますが、円周率がない時代では曲線図形である円の扱いに困っていました。
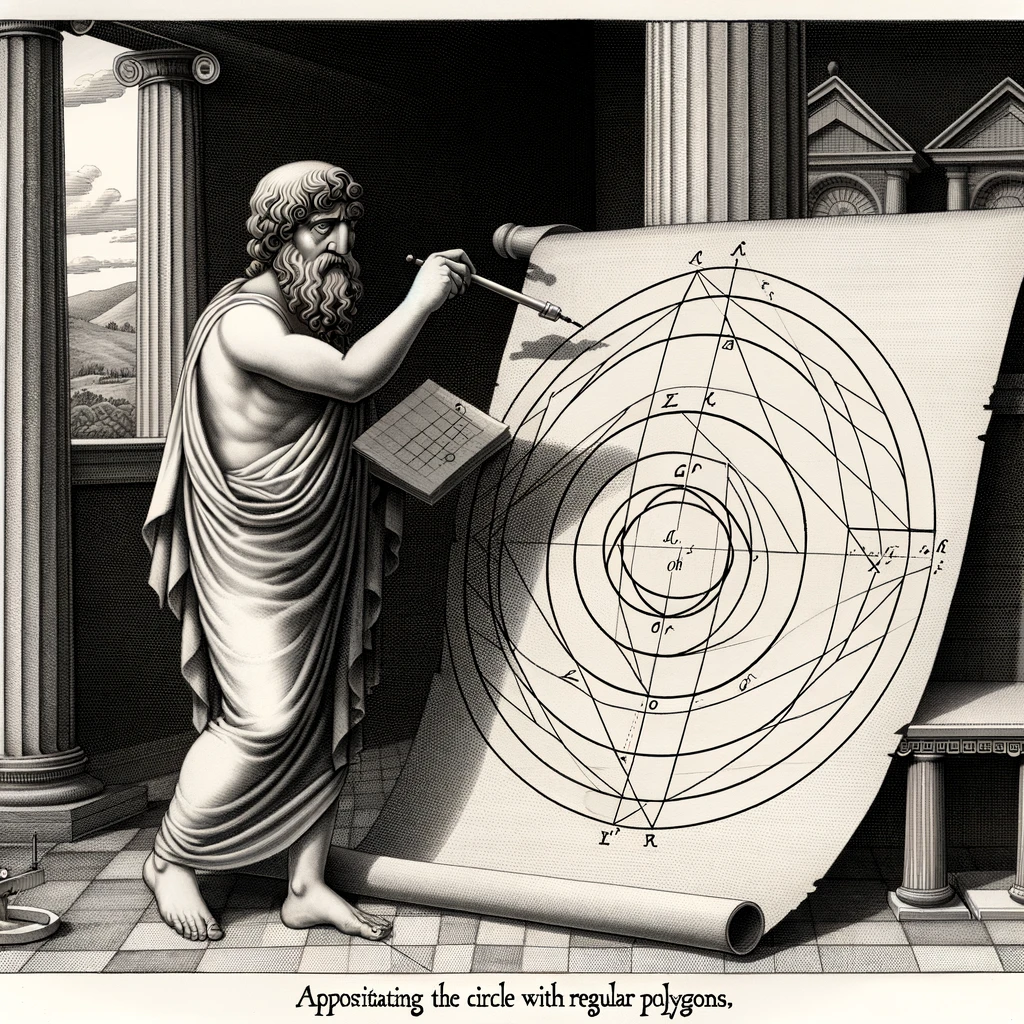
そこで、古代ギリシャの数学者アンティポンは、円を多角形で近似することで、円の面積を求めると同時に円積問題の解決を試みました。
この記事では、アンティポンの生涯と数学的な功績を現役数学教員がわかりやすく解説！
アンティポンの業績が後世の数学、特に円周率の近似値研究にどのような影響を与えたかを知ることができます。
この記事で主に扱っている時代と場所
この記事を読んでわかること
アンティポンの生涯
古代ギリシャの数学者アンティポン（Antiphon , B.C.5世紀）に関する情報は、プラトンの本や彼が書いたとされる『自然について』などに限られています。
＜図1＞ アンティポン（AIによるイメージ）
アンティポンの年譜
アンティポンの限られた情報を年譜にすると以下のようになります。
紀元前5世紀頃
アテネで研究を行う
円を多角形で近似することを試みる
わかっているのは紀元前5世紀に活躍したことだけ。
生年や没年について詳しいことはわかっていません。
アンティポンの活動場所
アンティポンは主に古代ギリシャのアテネで活動し、当時の学問の中心地であったアテネの学園で学び、哲学や数学の研究を行いました。
生地や没地は不明です。
コメント