エジプト、メソポタミア、インド、中国のそれぞれの文明で発生した数学。
しかし、古代文明の中で最も数学が栄えたのは、四大文明ではなくギリシャでした。
その要因の1つが、現在の数学の核である証明が生み出されたこと。
論証によって築かれたギリシャの数学はその後、インドやアラビアを経て近世ヨーロッパのルネサンスで復興し、現在の数学へとつながっています。
そんなギリシャの数学を、歴史の流れとともに年表にしたうえで、有名な数学者たちについてまとめました。
この記事を読むことで、古代ギリシャの数学の概要を掴むことができます。
| 時代 | 紀元前2000年頃~紀元前334年(アレクサンドロス大王の東方遠征まで) |
| 場所 | ギリシャ |
古代ギリシャの数学史年表
地中海地域、特にエーゲ海周辺で栄えた古代ギリシャ。
四大文明よりは遅咲きだったものの、紀元前の数学が最も発達した地域でした。
有力な文明が滅亡し、暗黒時代に突入する。
その後400年間は混乱の時代が続き、人々がエーゲ海周辺の島々に移住した。
人々が集住し、ポリスが誕生する。
ポリス内は法律で統治され、紀元前6世紀初頭には平民も議論に参加するようになった。
これにより、定理や公式を鵜呑みにすることなく、正しい理由を説明する土壌が整った。
ペロポネソス戦争が始まる。
アテネとスパルタの戦い。
戦争終盤、アテネに疫病が流行り始め、デロス神殿にて立方体倍積問題が出題される。
ギリシャがマケドニアに制圧される。
アレクサンドロス大王の父であるフィリッポス2世率いるマケドニアが、アテネとの戦争に勝った。
ギリシャにオリエントの文化が流れ込む
アレクサンドロス大王が東方遠征したことで、ギリシャに外国の文化が流れ込むようになった。
アレクサンドロス大王の東方遠征により、ギリシャ独自の文化が廃れていきます。
そのため、これ以降の時代をヘレニズム時代と呼び、エジプトのアレクサンドリアを中心に学問が栄えていくこととなりました。
古代ギリシャの数字
他の文明と同様、数学をする上で欠かせないのが数字。
古代ギリシャでは、文章を書くために使われていたギリシャ文字を数字にも転用しました。
- $~37~\cdots~\lambda~\zeta~$ ($~\lambda=30~,~\zeta=7~$)
- $~66~\cdots~\xi~$ϝ ($~\xi=60~,~$ϝ$=6~$)
- $~281~\cdots~\sigma~\pi~\alpha~$ ($~\sigma=200~,~\pi=80~,~\alpha=1~$)
- $~809~\cdots~\omega~\theta~$ ($~\omega=800~,~\theta=9~$)
上の例のように、各桁ごとに数字が割り当てられており、それらを並べることで数を表現できます。
大きな数を表すための記号も存在し、たくさんのギリシャ文字を並べて数を表しましたが、計算には不向きだったのは言うまでもありません。

古代ギリシャの数学者たち
この時代から「数学者」の名前が歴史に残っています。
多くの数学がエーゲ海周辺地域、さらにはアテネを中心に活躍をしたため、次の図解に示すように、互いに影響を及ぼし合いました。
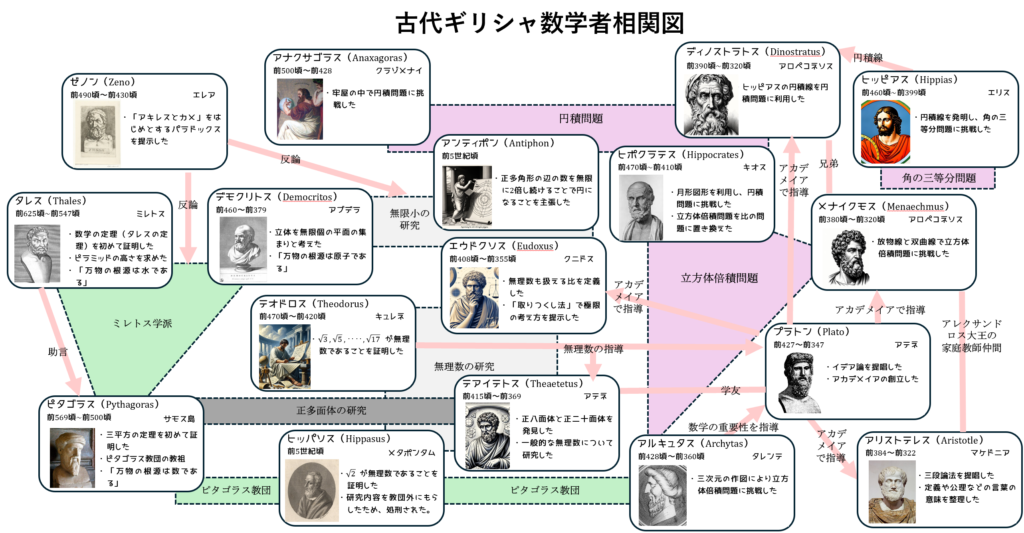
タレス:世界で最初の数学者
タレス(Thales , B.C.6525頃~B.C.547頃)は歴史に名が残っている最古の数学者です。

タレス
(出典:Unidentified engraver, Public domain, via Wikimedia Commons)
- 世界で初めて証明を行った。
- 相似を利用してピラミッドの高さや船までの距離をを求めた。
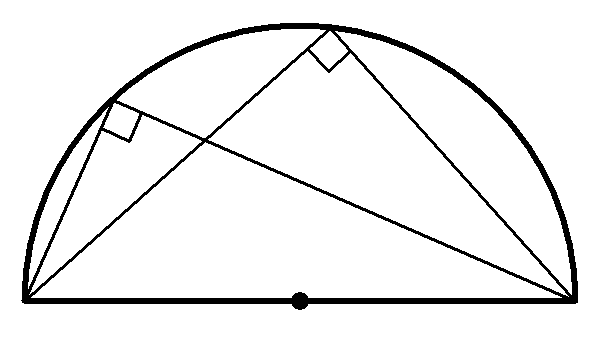
タレスが証明した定理は円に内接する三角形に関する定理で、「タレスの定理」と呼ばれています。
半円に内接する三角形は直角三角形である。

ピタゴラス:三平方の定理を証明した数学者
ピタゴラス(Pythagoras , B.C.569頃~B.C.500頃)は、タレスに次いで2番目に古い数学者です。

(出典:The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons)
- バビロニアでも知られていた三平方の定理を初めて証明した。
- 「ピタゴラス教団」を創設し、集団で数学の研究を行った。
- 数の分類を行った。
- 正四面体、正六面体、正十二面体を発見した。
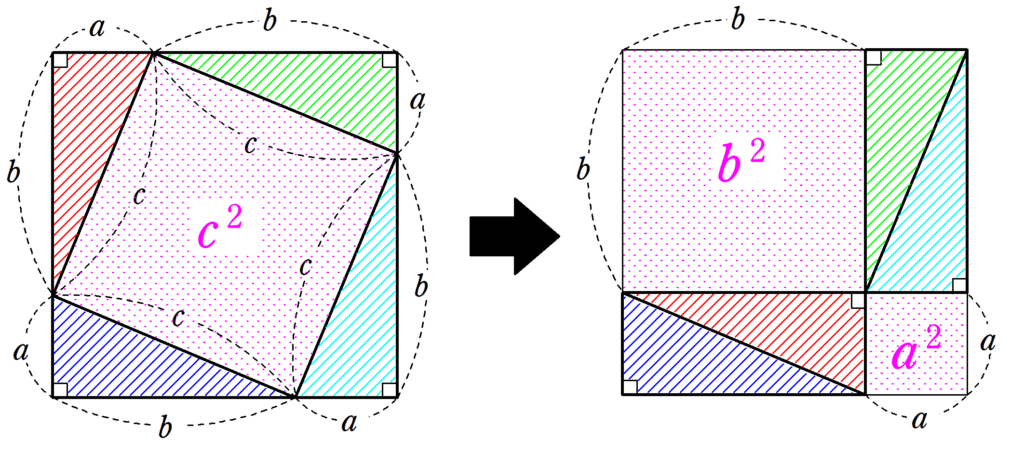
ピタゴラスが行った三平方の定理の証明方法は、図形を動かすだけの数式を使わない方法でした。

アナクサゴラス:円積問題を考え始めた天文学者
アナクサゴラス(Anaxagoras, B.C.500頃~B.C.428頃)は、三大作図問題の1つである円積問題を考え始めた天文学者として有名です。

(出典:Eduard Lebiedzki, after a design by Carl Rahl, Public domain, via Wikimedia Commons)
- 円積問題を考え始めた。
アナクサゴラスは太陽が石であると主張したがために、不敬罪に問われて牢屋に入れられます。
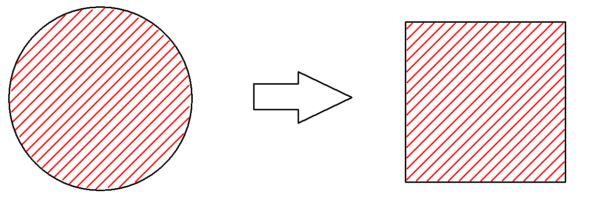
円積問題は、アナクサゴラスが牢屋の中で考えた問題でした。
1つの円の面積と等しい面積をもつ正方形を作図しなさい。


ゼノン:パラドックスを提起した哲学者
ゼノン(Zeno , B.C.490頃-B.C.430頃)は、パラドックス(矛盾)を提起した哲学者です。

(出典:Jan de Bisschop, CC0, via Wikimedia Commons)
- 運動に関するパラドックスを提起した。
- 無限を扱うことの難しさを数学界に投げかけた。
ゼノンが提起したパラドックスの中でも最も有名なのが、アキレスと亀のパラドックスです。
俊足のアキレスとゆっくり進む亀がいる。
亀がアキレスよりも前方にいるとき、アキレスは亀に追いつくことができない。
なぜなら、アキレスが亀のいた位置に追いつくときには、亀はまた前方に進んでしまっているからである。



これを繰り返していくため、アキレスはいつまで経ってもカメに追いつくことはできない。
当時の数学では、アキレスと亀のような無限と現実の齟齬を解消することができず、無限を扱うことの難しさが後の時代へと引き継がれました。

ヒッパソス:無理数を発見した数学者
ヒッパソス(Hippasus, B.C.5世紀中頃)は、ピタゴラス教団の一員で、無理数の存在を証明した数学者として知られています。

(出典:Boccanera G., Public domain, via Wikimedia Commons)
- $~\sqrt{2}~$が無理数であることを証明した。
「万物は数である」という信念のもと、この世のすべての数は自然数やその比(有理数)で表せるというピタゴラス学派の考えを、見事にくつがえす結果となりました。

テオドロス:無理数を拡張した数学者
テオドロス(Theodrous, B.C.465頃~ B.C.398頃)は、$~\sqrt{2}~$だけでなく、$~\sqrt{3}~$や$~\sqrt{17}~$といった数も無理数であることを証明しました。

- $~\sqrt{3}~,~\cdots~,~\sqrt{17}~$が無理数であることを証明した。
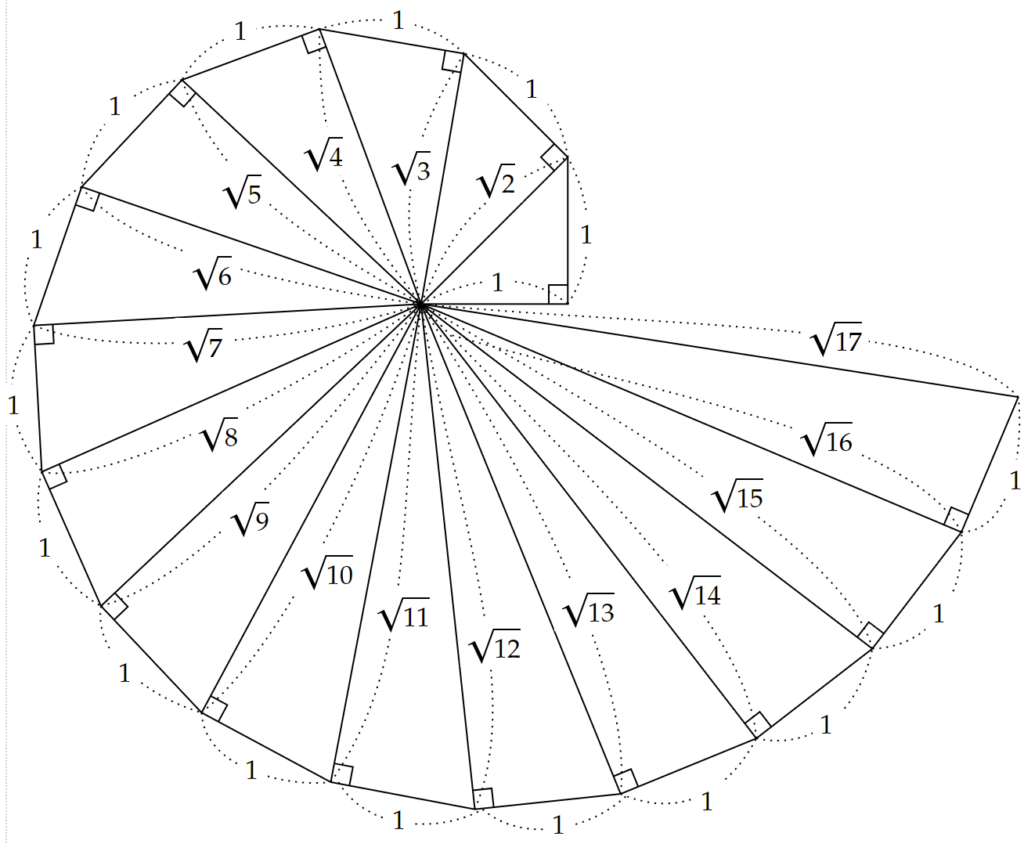
テオドロスの証明方法は明らかになっていませんが、テオドロスの螺旋と呼ばれる図形を用いたのではないかと推測されています。
図2のように、底辺$~1~$、高さ$~1~$の直角二等辺三角形から始まり、高さ$~1~$の直角三角形を組み合わせてできた図形をテオドロスの螺旋という。

ヒポクラテス:月形を研究した数学者
ヒポクラテス(Hippocrates , B.C.470頃-B.C.410頃)は、円積問題を解くために月形を研究した数学者です。

(出典:学生バイブ TVW, CC BY-SA 4.0, via Wikimedia Commons)
- 月形(ヒポクラテスの三日月)を研究し、円以外の曲線図形の面積を初めて求めた。
- 立方体倍積問題を比の問題に置き換えた。
ヒポクラテスは、2つの曲線図形の面積の和が直線図形の面積に変換できることを証明しました。
直角三角形について、各辺を直径とする半円を描く。
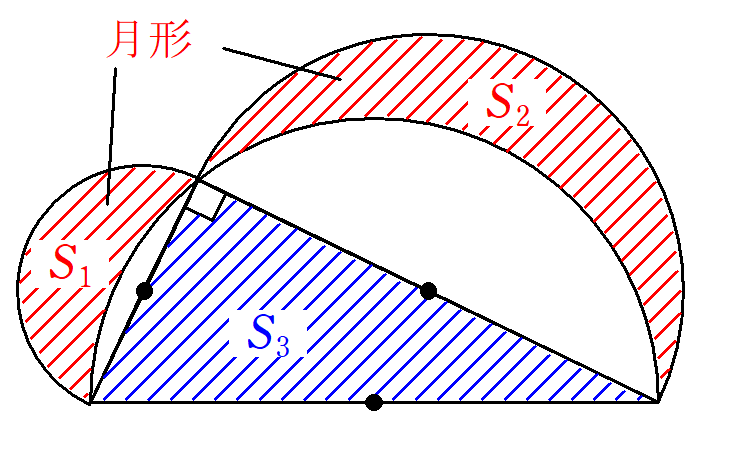
このとき、月形の面積の和と直角三角形の面積は等しくなる。
S_1+S_2=S_3
また、$~\sqrt[3]{2}~$の長さの作図にあたる立方体倍積問題を、次の条件を満たす$~x~$の作図へと問題をわかりやすく置き換えました。
1:x=x:y=y:2

デモクリトス:積分法の考え方を持っていた数学者
デモクリトス(Democritos, B.C.460頃~B.C.380頃)は、「万物は原子である」と説き、図形の無限分割を考えた数学者です。

- 錐体の体積は、柱体の体積の$~\displaystyle \frac{1}{3}~$であることを証明した。
- 立体を無限分割し、平面の面積の和として体積を考えた。
デモクリトスが提案した立体の無限分割は、17世紀のイタリアの数学者ボナヴェントゥーラ・カヴァリエーリ(Bonaventura Cavalieri , 1598年~1647年)と同様の考え方となります。
2つの立体を無限に細かく切断した際、各高さにおける切断面の面積が等しいとき、2つの立体の体積は等しい。
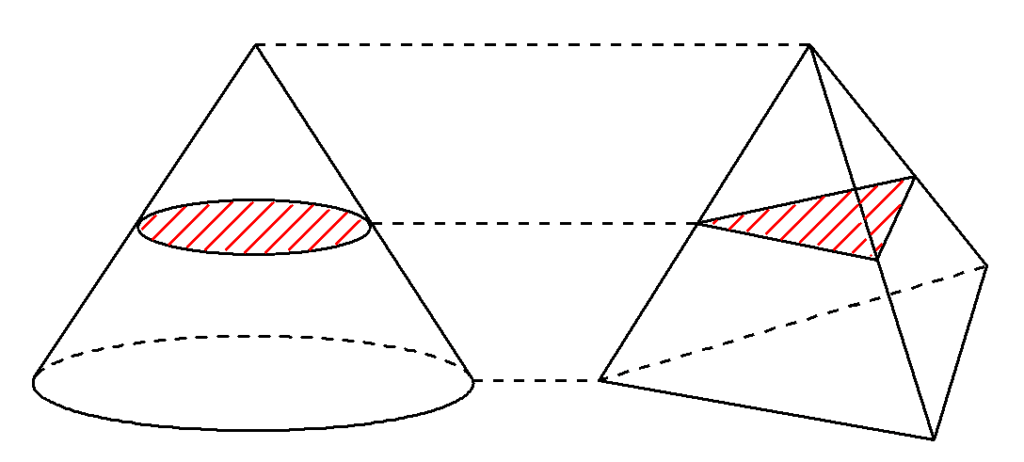
しかし、デモクリトスの無限に対する考え方はゼノンによって批判され、これ以降の数学界では無限を敬遠するようになりました。

ヒッピアス:円積線を発明した数学者
ヒッピアス(Hippias , B.C.460頃~没年不明)は、円積線と呼ばれる曲線を使って角の三等分問題の解決に挑んだ数学者です。

(AIによるイメージ)
- 円積線を用いて、角の三等分問題の解決に近づいた。
ヒッピアスが発明した円積線は、数学史上初の円以外の曲線でした。
今の数学を使えば以下のようなパラメータで表されます。
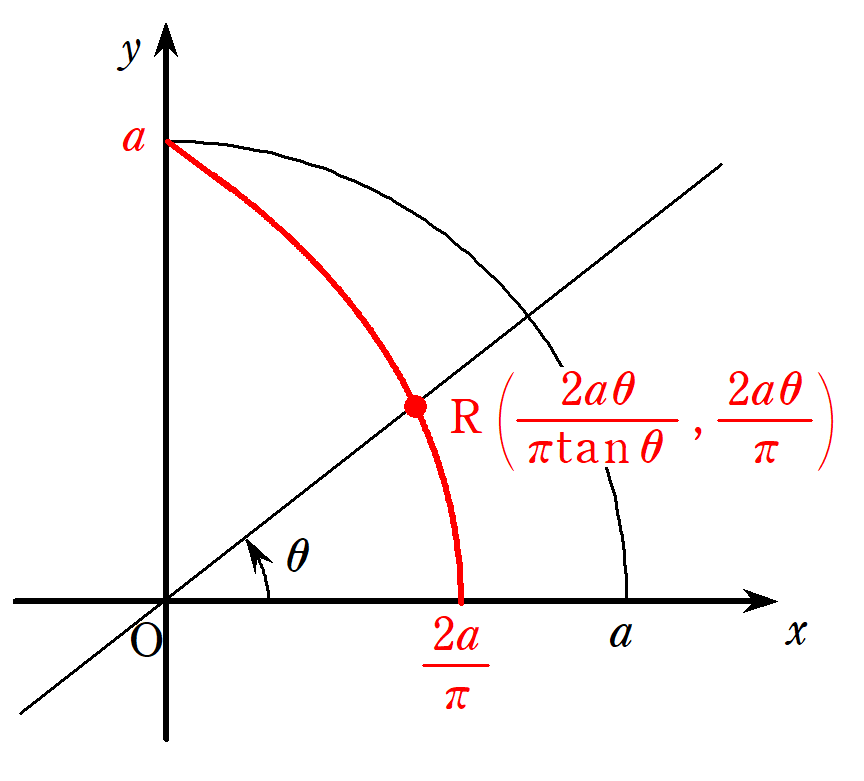
円積線の作図ができれば、角の三等分線はかけることがヒッピアスによって証明されましたが、円積線自体の作図が結局できず、ヒントを与えただけに留まりした。
また、円積線の研究はディノストラトスも行っています。

アンティポン:円を多角形で近似した数学者
アンティポン(Antiphon , B.C.5世紀)は、多角形を無限に細かくすれば円に近づくことを考えた数学者です。
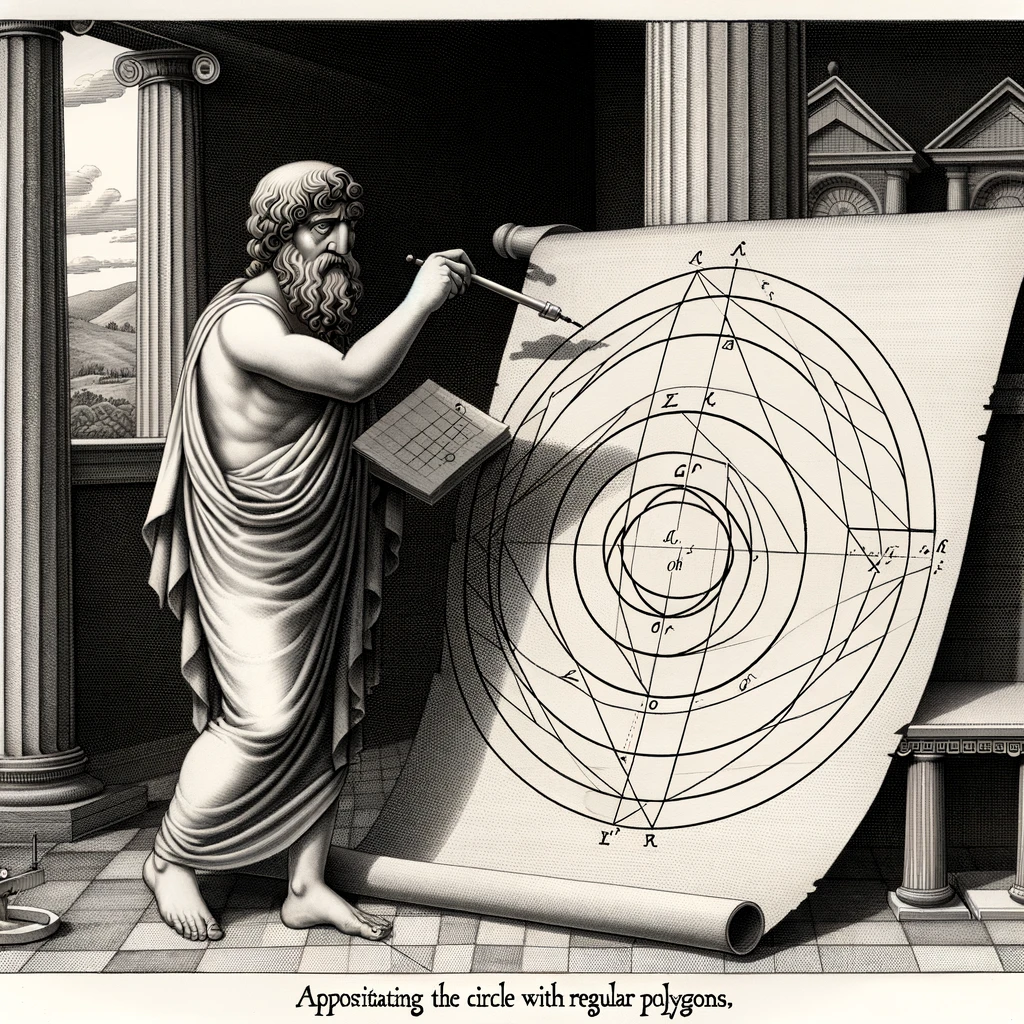
- 正多角形の辺の数を倍増させていくと、円に近づくことを考えた。
アンティポンは、この考え方を基に円積問題の解決に挑んだものの、無限回の操作は作図のルールに反していました。
しかし、正多角形を分割していくという考え方は、エウドクソスの取り尽くし法やアルキメデス以降の円周率計算に利用されることになります。

アルキュタス:3次元の作図を考えた数学者
アルキュタス(Archytas , B.C.428頃~B.C.360頃)は、立方体倍積問題を解決するために、3次元空間での作図による解法を与えた数学者です。

(出典:From Wikimedia Commons, the free media repository)
- 空間内の作図により、立方体倍積問題を解決しようとした。
ヒポクラテスが提案した比による$~\sqrt[3]{2}~$の表し方を、空間内の作図で実現しました。
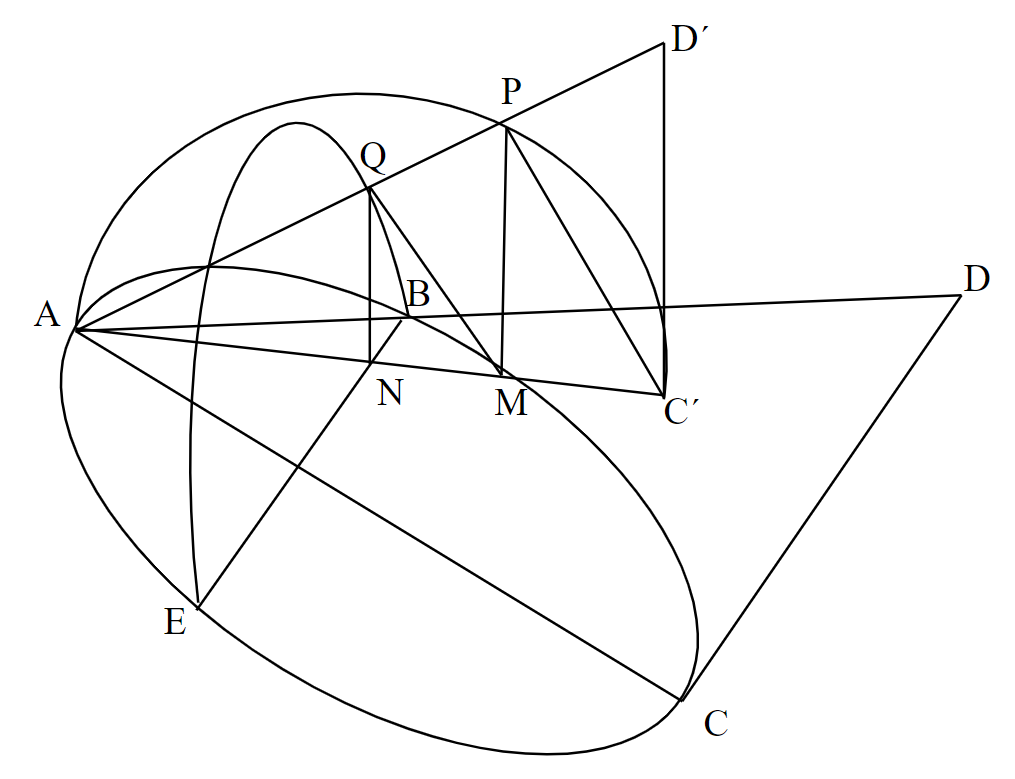
立体の作図は、作図のルールに反していたため、立方体倍積問題の解決とは言えませんでした。

プラトン:数学を育てる土壌を築いた哲学者
プラトン(Plato , B.C.427頃~B.C.347頃)は、数学の重要性を説き、学園アカデメイアで数学者の育成に貢献した哲学者です。

(出典:Unidentified engraver, Public domain, via Wikimedia Commons)
- 真理を追究する手段として、数学の重要性を説いた。
- 学園アカデメイアを創設し、エウドクソスなどの数学者たちを育てた。
幾何学で必要な論理的思考力を重視したアカデメイアで、エウドクソスやディノストラトス、メナイクモスといった数学者や、哲学者アリストテレスを育てました。


テアイテトス:無理数と正多面体を研究した数学者
テアイテトス(Theaetetus ,B.C.417頃〜B.C.369頃)は、ヒッパソスやテオドロスの無理数の発見や、ピタゴラスの正多面体の研究を拡張させた数学者です。

(AIによるイメージ)
- 一般的な無理数について、ユークリッドの互除法と同じ方法で比を考えた。
- 正八面体と正二十面体を発見し、正多面体が5種類であることを証明した。
テアイテトスは過去の数学者たちの発見を次のように拡張しています。
| 分野 | 無理数 | 正多面体 |
| テアイテトス以前 | 紀元前5世紀中頃、ヒッパソスが$~\sqrt{2}~$の無理数性を証明する。 紀元前5世紀後半、テオドロスが$~\sqrt{3}~$や$~\sqrt{17}~$の無理数性を証明する。 | 紀元前6世紀後半、ピタゴラスが正4,6,12面体を発見する。 |
| ↓ | ↓ | |
| テアイテトスの功績 | 紀元前4世紀前半、テアイテトスが無理数の証明の一般化を行う。 | 紀元前4世紀前半、テアイテトスが正8,20面体を発見する。 |

エウドクソス:取りつくし法と比例論を研究した数学者
エウドクソス(Eudoxus ,B.C.408頃〜B.C.355頃)は、ヘレニズム以前の数学者の中で最も独創的な発想力を持った数学者として知られています。

(AIによるイメージ)
- 取り尽くし法によって、曲線図形の面積を求める術を得た。
- 比を定義し、無理数も他の数と同様に計算できることが示された。
取り尽くし法は積分の考え方、比例論は実数の連続性の考え方へとつながっており、約2000年後の数学界に引けをとらない発想を持っていたことがわかります。
ある量からそれの半分以上を取り去り、その残りからその半分以上を取り去る。
さらにこれを続けていけば、あらかじめ与えられたいかなる小さな量よりも小さい量が残る。
4つの数量$~a~,~b~,~c~,~d~$に対して、与えられた整数$~m~,~n~$について、
\begin{cases}
ma < nb &ならば~~~~mc < nd \\
ma = nb &ならば~~~~mc = nd \\
ma > nb &ならば~~~~mc > nd
\end{cases}のいずれかが必ず成り立つとき、$~\displaystyle \frac{a}{b}=\frac{c}{d}~$である。

ディノストラトス:円積線を円積問題に利用した数学者
ディノストラトス(DIinostratus , 紀元前 390年頃〜紀元前320年頃)は、円積線によって円積問題が解けることを証明した数学者です。

(AIによるイメージ)
- 円積線を円積問題に応用した。
ヒッピアスが角の三等分問題のために発明した円積線について、以下のような性質をディノストラトスは見つけました。
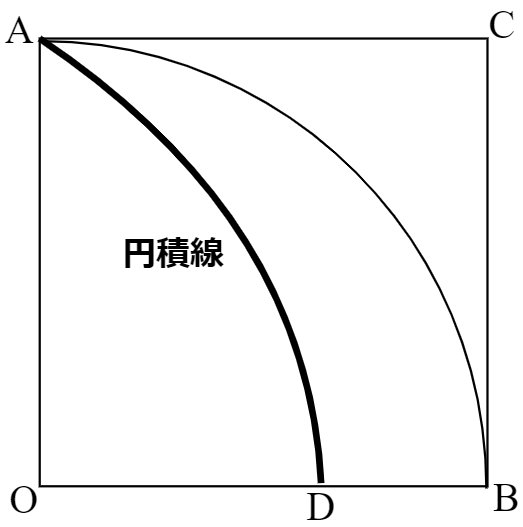
上の図において、
\stackrel{\large\frown}{AB} ~:~OB~=~OB~:~ODこの性質を利用することで、円積問題も解決するため、円積線の作図への注目度が上がりました。

メナイクモス:円錐曲線を立方体倍積問題に利用した数学者
メナイクモス(Menaechmus , 紀元前 380年頃〜紀元前320年頃)は、ディノストラトスを兄に持ち、自身は立方体倍積問題の解決に挑んだ数学者です。

(AIによるイメージ)
- 円錐曲線を使えば、$~\sqrt[3]{2}~$の長さが作図できることを示した。
関数と座標がない時代、メナイクモスは幾何的に$~\sqrt[3]{2}~$の長さが出ることを証明しました。
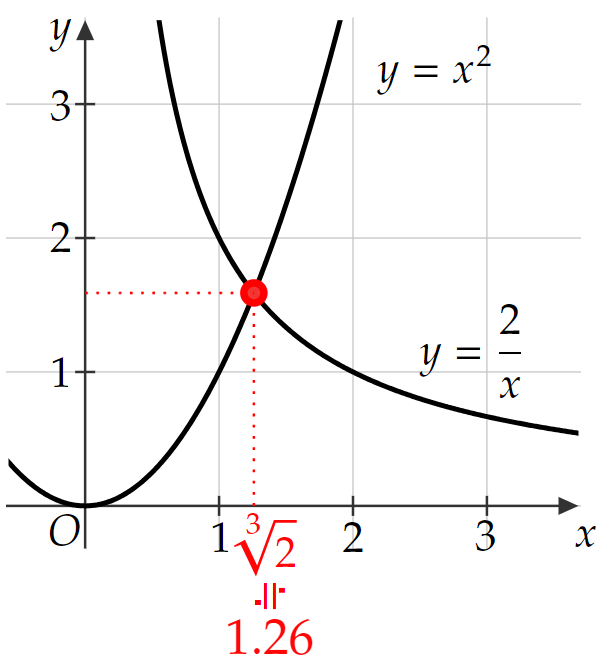
彼が考えた解法の1つは、以下のような放物線と双曲線の交点を利用したものです。
放物線$~y=x^2~$と双曲線$~\displaystyle y=\frac{2}{x}~$の交点の$~x~$座標が$~\sqrt[3]{2}~$である。

アリストテレス:数学用語の整理をした哲学者
アリストテレス(Aristotle , 紀元前 384年〜紀元前322年)は、時の支配者アレクサンドロス大王の家庭教師も務め、論理学に力を入れていた哲学者です。

(出典:After Lysippos, Public domain, via Wikimedia Commons)
- 三段論法を定義した。
- 公理、公準、定義、定理といった数学用語を整理した。
世界初の証明から200年以上経ち、曖昧になってきていた証明に関する用語を、アリストテレスはきちんとまとめ直しました。
公理:証明なしでも誰もが正しいと認めること。
公準:特定の分野の中で、要請される前提(誰もが正しいと認めるものに限る)。
定義:新たに与えられる言葉の意味を示したもの。
定理:定義や公理、公準や証明済みの定理から証明されること。
(実際は、証明された命題の中で重要度の高いものを定理と呼ぶ。)

数学の土台が築かれた時代だった
証明が誕生し、数学の根幹が築かれたギリシャの数学。
この時代の数学は、紀元前300年頃のユークリッドの『原論』にまとめられ、数学の土台として後世に君臨し続けています。
ヘレニズム時代に入ってからは、学問の中心地がアテネからアレクサンドリアに移り、ギリシャで培われた数学をさらに発展させる数学者たちが生まれることとなりました。

この時代の数学者の名前は「〇〇ス」が多いね!



その時代の文法に従っていたんだ。
ちなみに、「プラトン」はニックネームで、本名は「アリストクレス」だよ。
ただ、ゼノンやアンティポンも別の名前があるのかもしれないね。

コメント