【数学史５－５】『九章算術』での円周率は3?　実用的な観点で円や弓形を研究していた！

　紀元前に誕生し、中国数学の体系を完成させた『九章算術』。

　『九章算術』の1章「方田」では、円形の田んぼが扱われており、当時使われていた円周率や円の面積の求め方が載っていました。

　この記事では、古代中国で研究された円や弓形図形について解説。

　当時、実は、円周率は$~3~$で計算され、半径を使った円の面積の求め方はありませんでした。

古代中国の円周率

　『九章算術』は紀元前2世紀頃に書かれ、その後の中国数学を体系立てた数学書です。

　全9章の中の第1章は「方田」で、様々な形の田んぼの面積を求め方が載っていました。

　その中に円形の田んぼも登場するため、古代中国における円の扱われ方を知ることができます。

あわせて読みたい

【数学史５－１】古代中国の数学の記録は紀元前200年頃から！それ以前の記録がない理由を解説！ 四大文明の1つである中国。中国の歴史は紀元前6000年頃から始まっているものの、数学書に関しては紀元前213年以前のものがありません。その理由は、秦の始皇帝の焚書政策であり、その後に書かれた『周髀算經』と『九章算術』が古代中国数学を物語る書物となっています。この記事では、紀元前の中国の歴史の流れと、古代中国の2冊の数学書について解説します。

古代中国の円周率は3

　『九章算術』では、円周率そのものを求める問題は無かったものの、問題文の中に円周率がいくつなのかわかる記述がありました。

　円の面積の求め方に関しては後述するとして、今回注目すべきなのは１行目です。

　「円周$~30~$歩、直径$~10~$歩の円田」ということから、古代中国の円周率は

円周率=\frac{円周}{直径}=\frac{30}{10}=3

とわかります。
 
　円周率が$~3~$というのは、円と正六角形の周の長さが等しくなってしまうことを意味します。

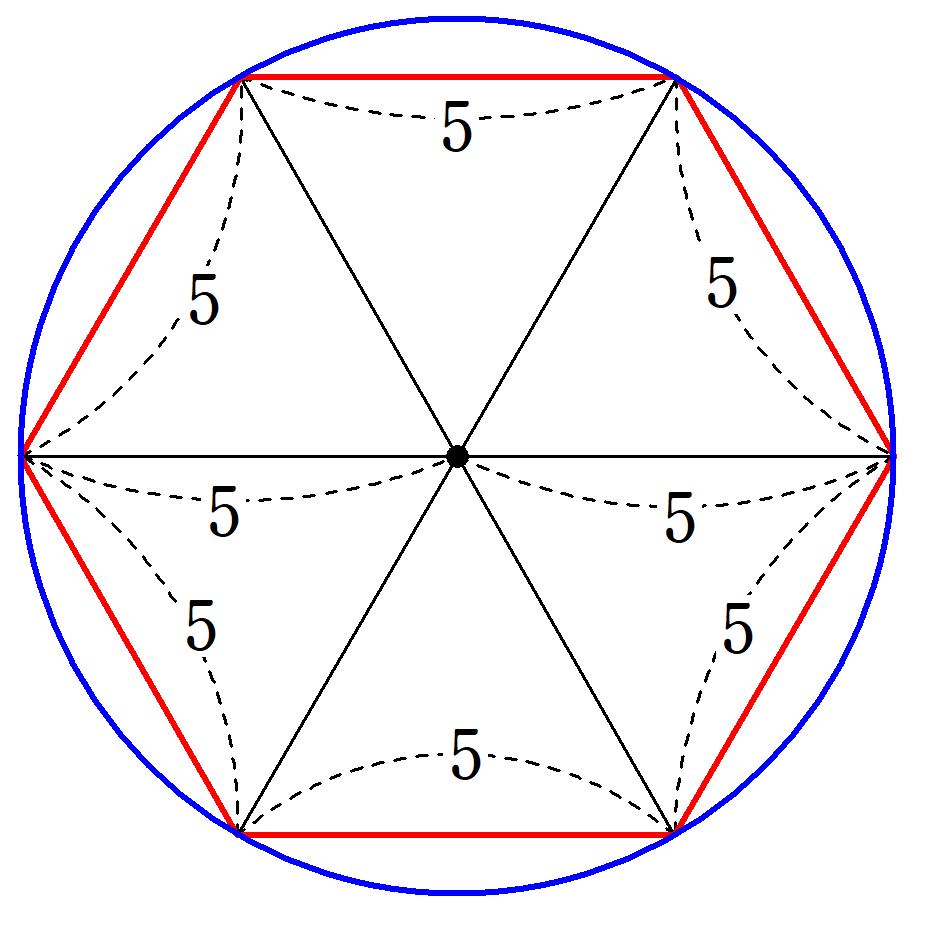
精度よりも計算の利便性が重視

　この時代よりも約1500年ほど昔のエジプトでは、円周率は$~\displaystyle \frac{256}{81} \fallingdotseq 3.16~$と求められていました。

　それに対し、連立方程式や負の数を操っていた紀元前200年頃の中国の円周率が$~3~$というのは違和感があるでしょう。

　しかし、現実の問題を解決する上では十分正確で、とにかく計算がしやすいという理由で円周率$~3~$が用いられ続けました。

古代中国の円の面積公式

　『九章算術』では、円周率そのものを求める問題や、円の面積公式を導くような問題はありませんでした。

　そのため、与えられた公式を使って各問題を解いています。

円の面積は4通りで求められた

先の『九章算術』1章第31問をはじめとする円の面積の求め方について、次のような４つの公式が同書の中にありました。

S=\frac{\ell}{2}\cdot \frac{d}{2}

S=\frac{\ell \cdot d}{4}

S=\frac{d^2 \cdot 3}{4}

S=\frac{\ell^2}{12}

　現在のように半径を使うのではなく、測量がしやすい円周や直径を使っている点が実用的と言えます。
 
　②～④の公式は、①の公式から順々に証明することができます。

S=\frac{\ell}{2}\cdot \frac{d}{2}=\frac{\ell \cdot d}{4}

S=\frac{3d \cdot d}{4}=\frac{d^2 \cdot 3}{4}

S=\frac{\ell \cdot \frac{\ell}{3}}{4}=\frac{\ell^2 }{12}

　ちなみに、円の面積の公式が4つ存在した理由は、与えられた情報に応じて、一番計算がしやすいものを選べるようにするためです。

面積の求め方の有力説1：おうぎ形に分割

　　4つの公式のもとになっている①の公式は、どのように発見されたのでしょうか？

　『九章算術』をはじめとする書物にその過程は載っていないものの、現在２つの説が考えられています。

　そのうちの1つはおうぎ形に分割していくだけの方法です。

『九章算術』の円の面積の求め方①の導出1

　図2の円周$~\ell~$、直径$~d~$の円を、図2のように分割する。

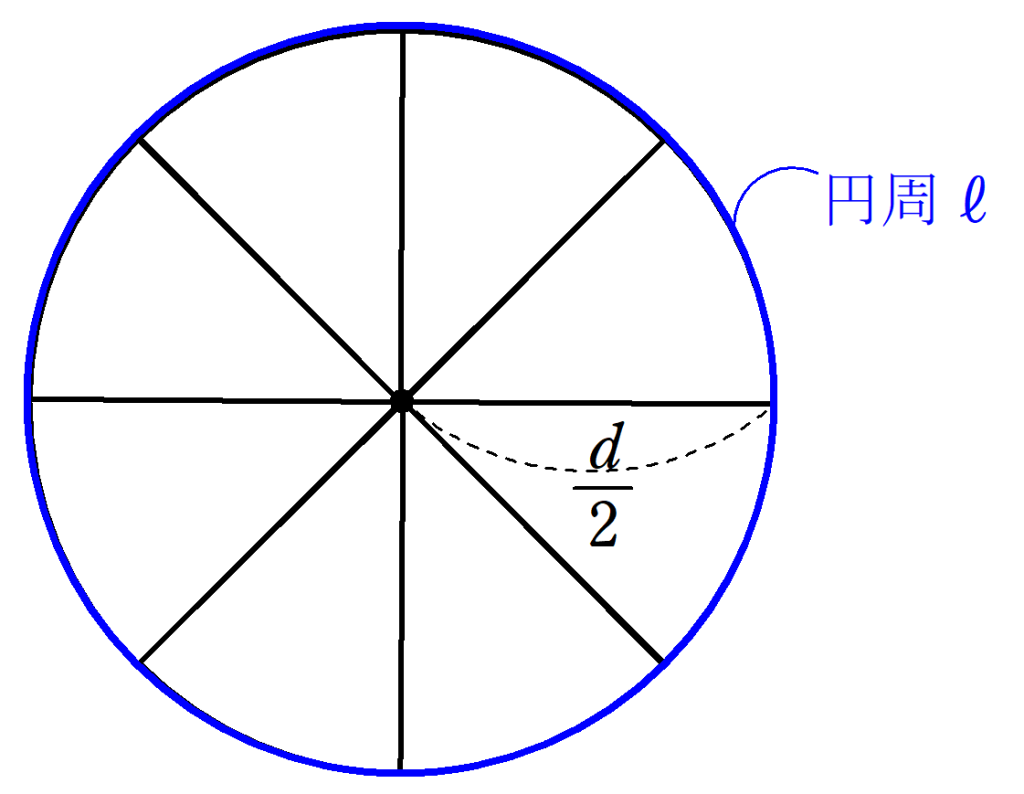
　分割してできたおうぎ形を、図3のように上下交互に並べる。

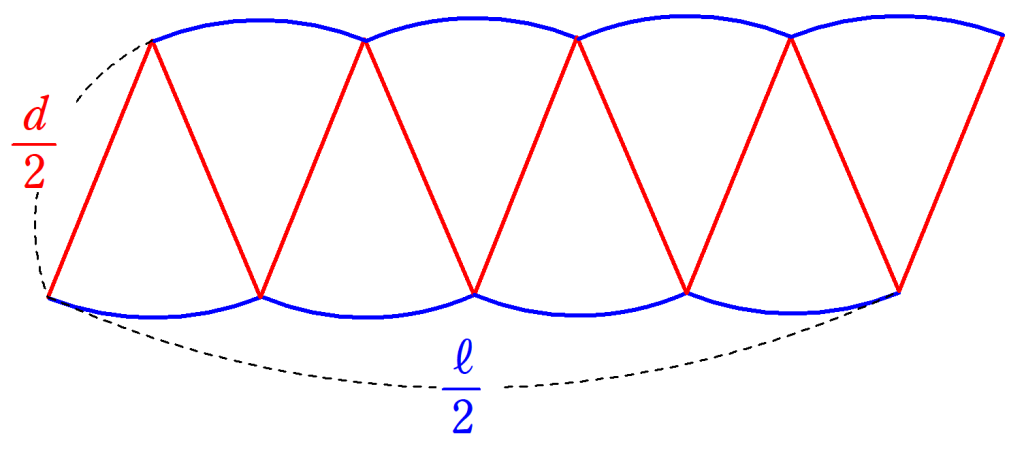
　細かく分割するほど、長方形に近づくため、円の面積$~S~$は

S=\frac{\ell}{2}\cdot \frac{d}{2}

と求まる。

　現在でも使われている、よくある証明方法です。

面積の求め方の有力説2：円の切り開く

　もう1つの方法は、中世の中国の文献に載っていた求め方です。

『九章算術』の円の面積の求め方①の導出2

　円周$~\ell~$、直径$~d~$の円の内部に、同じ中心を持ち、半径が異なる円を無数に作る。

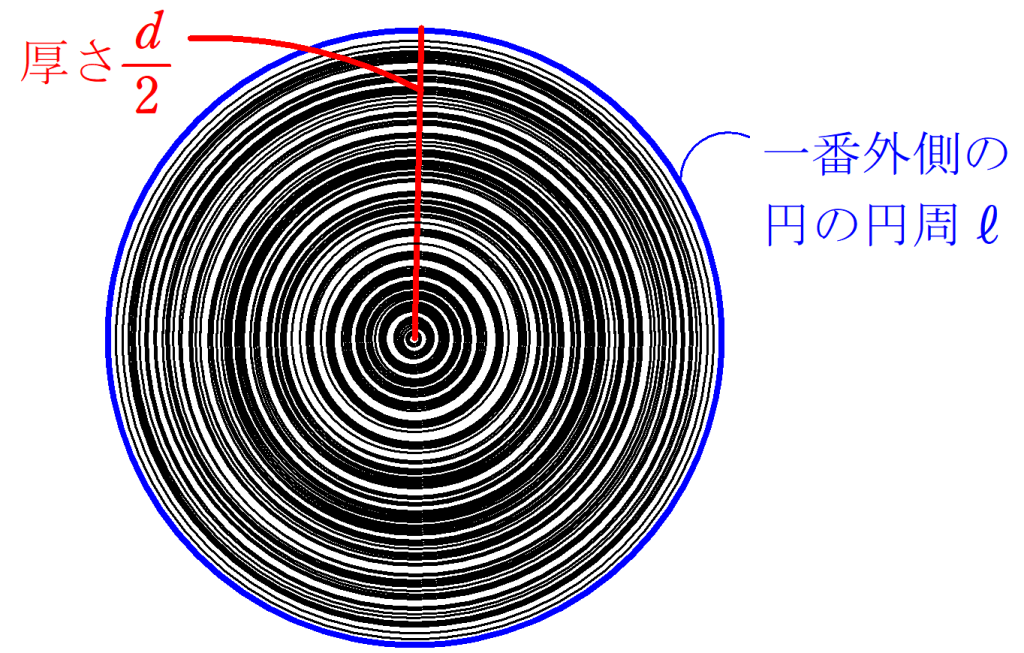
　これらの円を赤線で切り、各円の円周を伸ばすと、図5のような二等辺三角形が出来上がる。

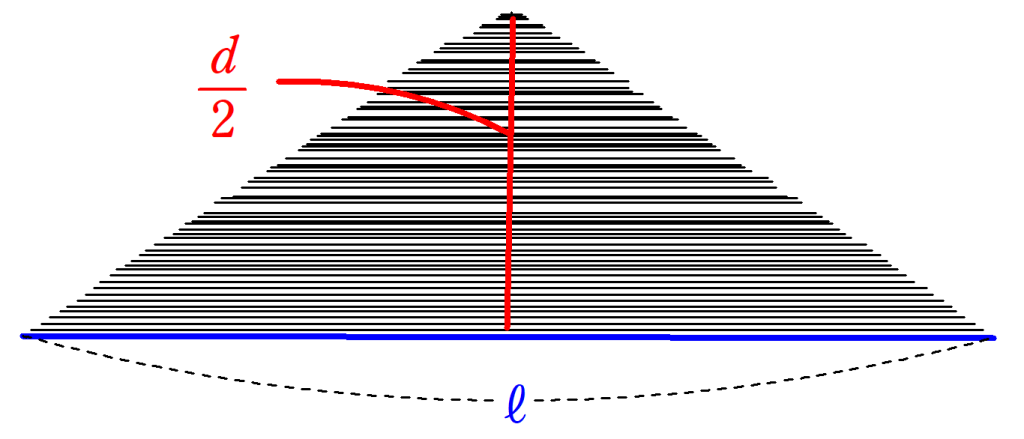
　したがって、円の面積$~S~$は

S=\frac{1}{2} \cdot \ell \cdot \frac{d}{2}=\frac{\ell}{2}\cdot \frac{d}{2}

と求まる。

　どちらの求め方も$~\displaystyle \frac{\ell}{2}\cdot \frac{d}{2}~$という式が直接出ているため、有力な説と言われているのでしょう。

弓形の面積公式

　今の数学教育で主だって登場することはない弓形の面積についても、『九章算術』では公式を与えていました。

　弓形というのは、円の弧と弦で囲まれた部分のことです。

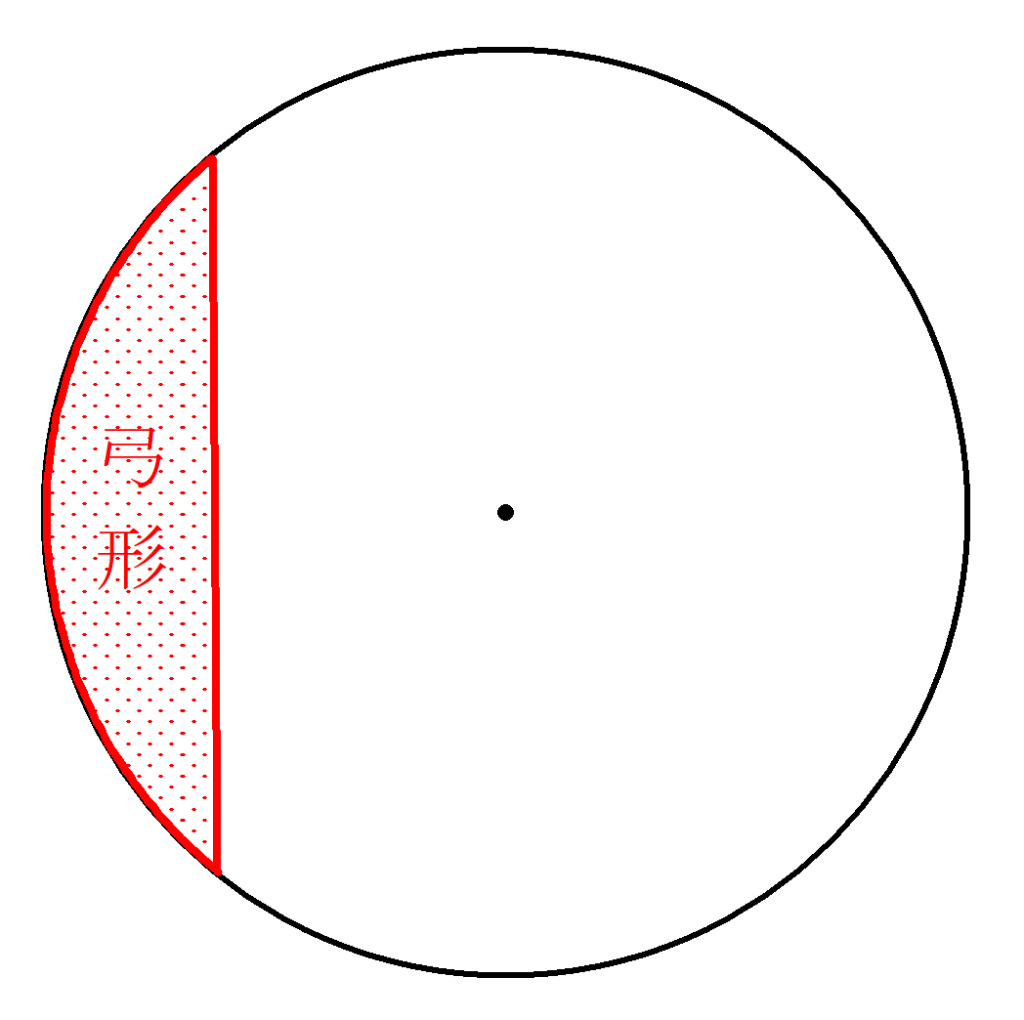
弦の長さと矢の長さで求めることができる

　『九章算術』1章第35問では、「弧田術」として、次のような求め方が載っています。

『九章算術』の円の面積の求め方

　弦の長さを$~s~$、矢（弦の中点から弧に対して垂直に伸ばした線分）の長さを$~a~$とすると、弓形の面積$~S~$は次のように求められる。

S=\frac{as+a^2}{2}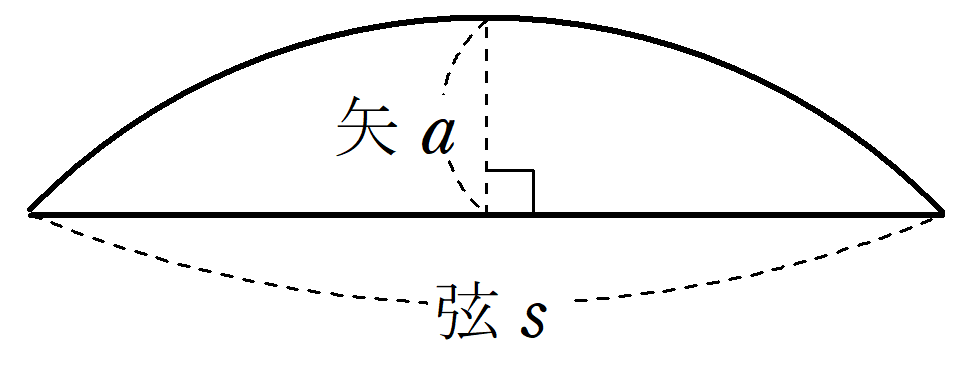

　ただし、この公式が正しいのは半円のときのみでした。

　実際この条件で、弓形の面積を正しく求めようとすると、

S=\left(\frac{s^2}{8a}+\frac{a}{2}\right)^2\cdot \sin^{-1}{\left( \frac{4as}{s^2+4a^2} \right)}-\frac{s^3-4a^2s}{16a}

という複雑な式が必要となります。

台形で近似をしている

　『九章算術』の弓形の面積公式が正確でない理由は、弓形を台形で近似していたからです。

　弓形の公式を紐解いてみましょう。

弓形の面積の求め方

　弦の長さが$~s~$、矢の長さが$~a~$の弓形を、図8のような台形で近似する。

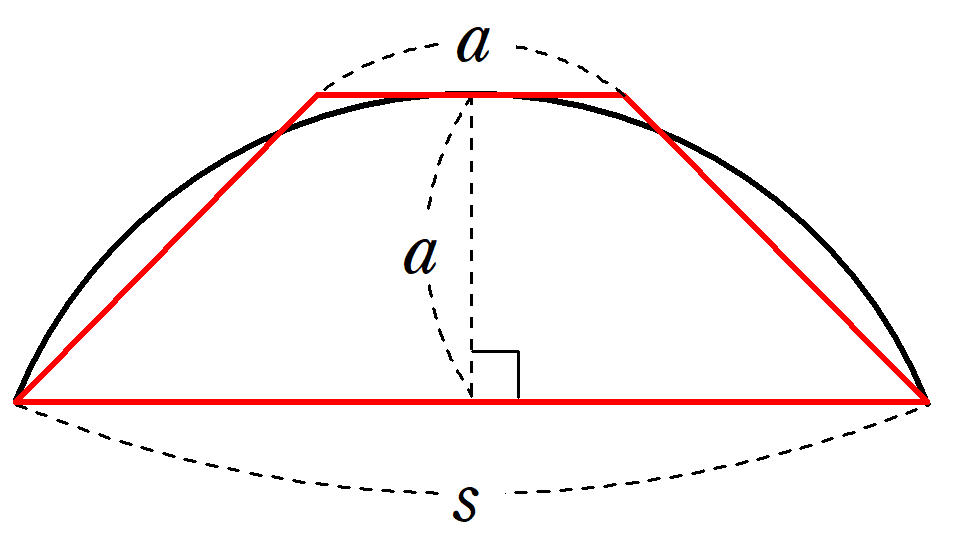
　このとき、台形で近似した弓形の面積$~S~$は

\begin{align*}
S&=(a+s)\cdot a\cdot \frac{1}{2}  \\
\\
&=\frac{as+a^2}{2}  
\end{align*}

と求まる。

　図8からもわかるように、弓形を台形と見立てるには少々雑です。

　ただ、円周率と同様に現実の問題を解決する上では十分正確で、とにかく計算がしやすいという利点がありました。

半円ならば正確に求まる

　雑な近似である弓形の面積の公式も、半円であれば正確に求まります。

　『九章算術』の弓形の問題の中で、半円の場合に関するものがありました。

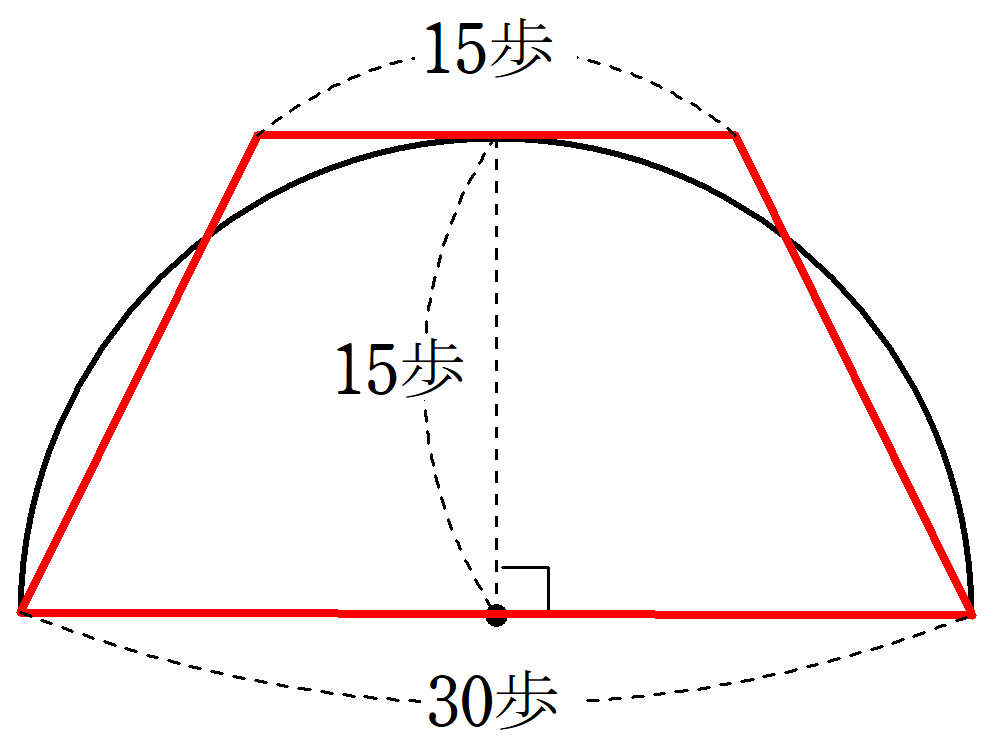
　この問題の答えは$~1~$畝^※2$~\displaystyle 97\frac{1}{2}~$平方歩と書かれており、以下のような計算が「弧田術」（弓形の面積の公式）によって行われています。

※2「畝」は現在でも使われている面積の単位で、1畝＝240平方歩。

　実際に『九章算術』の弓形の面積の求め方を使って計算すると、

\begin{align*}
&~~~\frac{15\cdot 30+15^2}{2}  \\
\\
&=\frac{675}{2}~~~(平方歩)\\
\\
&=337~\frac{1}{2}~~~(平方歩)\\
\\
&=1(畝)~~97~\frac{1}{2}~~~(平方歩)\\
\end{align*}

であり、直径$~d=30~$歩の半円として、『九章算術』の円の面積の求め方③を使うと、

\begin{align*}
&~~~\frac{30^2 \cdot 3}{4}\cdot \frac{1}{2}  \\
\\
&=\frac{2700}{8}  \\
\\
&=\frac{675}{2}~~(平方歩)
\end{align*}

となるため、円周率が$~3~$という条件の下、弓形の面積の公式は半円ならば正確であるとわかります。

まとめ・参考文献

　古代中国における円の考え方について解説しました。

• 古代中国の数学書『九章算術』での円周率は$~3~$であった。
• 円の面積を求めるうえで、正確さよりも計算の利便性が重視された。
• 弓形の面積についても近似の考え方から公式を与えていた。

　エジプトやバビロニアと同じように、古代中国でも正確な数値より計算上の便利さを優先していました。

　次の記事では、古代中国の平方根について解説します。

次の記事へ

【数学史５－６】平方根は有限のみ対応！『九章算術』の開平法とは？ 　紀元前2世紀頃にでき、中国数学を体系立てた数学書である『九章算術』。その4章は、正方形の面積から一辺の長さを求める問題が載っており、図形を用いた開平算の方法が扱われていました。この記事では、その平方根を求める方法を中心に、4章「少広」の様々な問題について解説します。

この章のまとめへ

【数学史まとめ５】古代中国の数学 　四大文明の一つで長い歴史を持つ中国。 　しかし、紀元前213年の焚書政策により、紀元前の数学関係の資料はほとんど失われてしまいました。 　そのため、古代中国の数…

　弓形を台形に近似するってセンスあるよね。半円だと一致しているし。

厳密にいえば、円周率を$~3~$とした場合の話だよ。
　$~3.14~$で計算した場合には、弓形の公式で半円を計算しても一致しないから注意しよう。