他の年度については、コチラからどうぞ。
サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
解説の内容自体に影響はありません。
問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。
3
(1) 頂点: $~(a,3a^2-3)~$ 、軸: $~x=a~$
(2) $~a < 0~$ のとき、$4a^2-3(x=0)~$
$~0 \le a < 4~$ のとき、$3a^2-3(x=a)~$
$~a \ge 4~$ のとき、$4a^2-8a+13(x=4)~$
(3) $~a=-1~$ のとき、最大値は$25(x=4)$
$~\displaystyle a=\frac{2\sqrt{3}}{3}~$ のとき、最大値は$\displaystyle \frac{55-16\sqrt{3}}{3}(x=4)$
(1) 頂点: $~(a,3a^2-3)~$ 、
軸: $~x=a~$
(2) $~a < 0~$ のとき、
$~4a^2-3(x=0)~$
$~0 \le a < 4~$ のとき、
$~3a^2-3(x=a)~$
$~a \ge 4~$ のとき、
$~4a^2-8a+13(x=4)~$
(3) $~a=-1~$ のとき、
最大値は$25(x=4)$
$~\displaystyle a=\frac{2\sqrt{3}}{3}~$ のとき、
最大値は$\displaystyle \frac{55-16\sqrt{3}}{3}(x=4)$
3(1)
平方完成により、式変形していくと、
\begin{align}
f(x)&=x^2-2ax+4a^2-3 \\
&=(x-a)^2-a^2+4a^2-3 \\
&=(x-a)^2+3a^2-3
\end{align}
となる。
よって、頂点の座標は $~(a,3a^2-3)~$ 、軸の方程式は $~x=a~$ と求まった。
3(2)
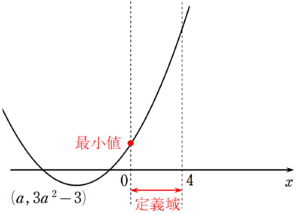
軸の位置で場合分けをする。
① $~a < 0~$ のとき
グラフは次のようになる。
グラフから、最小値は $~x=0~$ のときである。
\begin{equation}
f(0)=4a^2-3
\end{equation}
よって、最小値は求まった。
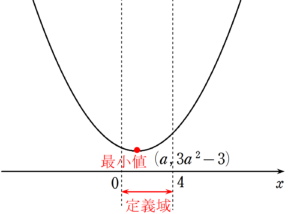
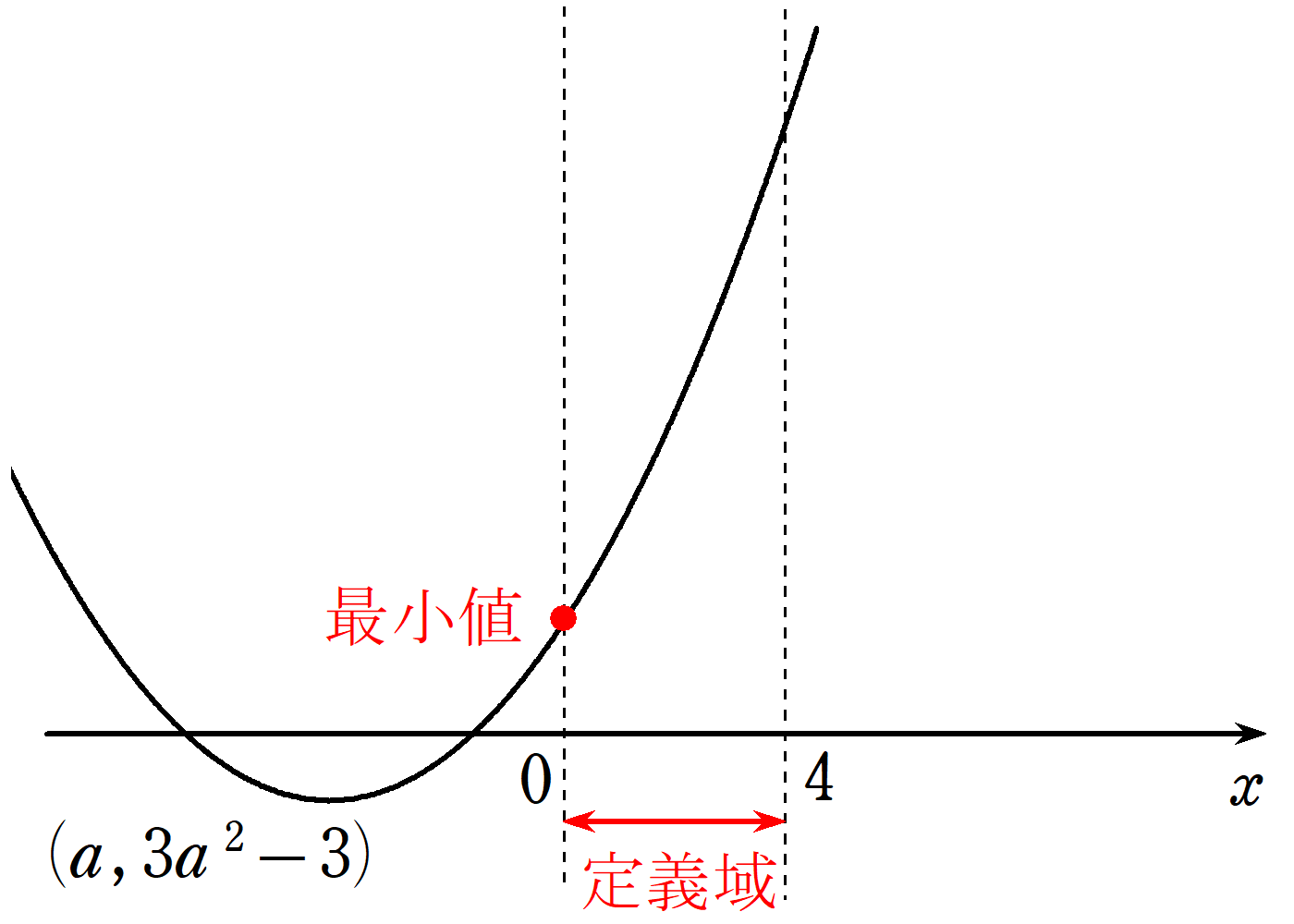
② $~0 \le a < 4~$ のとき
グラフは次のようになる。
グラフから、最小値は頂点( $~x=a~$ )となる。
\begin{equation}
f(a)=3a^2-3
\end{equation}
よって、最小値は求まった。
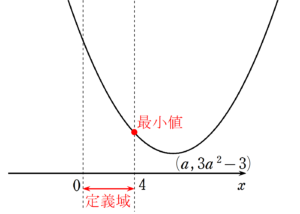
③ $~a \ge 4~$ のとき
グラフは次のようになる。
グラフから、最小値は $~x=4~$ のときである。
\begin{align}
f(4)&=4^2-2a\cdot 4+4a^2-3 \\
&=16-8a+4a^2-3 \\
&=4a^2-8a+13
\end{align}
よって、最小値は求まった。
以上①~③をまとめると、
\begin{cases}
a < 0のとき、&4a^2-3(x=0) \\
0 \le a < 4のとき、&3a^2-3(x=a) \\
a \ge 4 のとき、&4a^2-8a+13(x=4)
\end{cases}
\begin{cases}
a < 0のとき、&4a^2-3(x=0) \\
0 \le a < 4のとき、&3a^2-3(x=a) \\
a \ge 4 のとき、&4a^2-8a+13(x=4)
\end{cases}
が求まった。
※ $~a~$ の場合分けにおいて、 $~a \le 0,0 < a < 4,4 \le a~$ などにしても、OKです。
3(3)
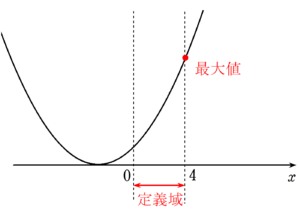
(2)の場合分けに基づいて、最小値が $~1~$ となるときの $~a~$ を求める。
① $~a < 0~$ のとき
\begin{align}
4a^2-3&=1 \\
4a^2&=4 \\
a^2&=1 \\
a&=\pm 1
\end{align}
であり、 $~a < 0~$ から、 $~a=-1~$ 。
② $~0 \le a < 4~$ のとき
\begin{align}
3a^2-3&=1 \\
3a^2&=4 \\
\\
\displaystyle a^2&=\frac{4}{3} \\
\\
a&=\pm \frac{2}{\sqrt{3}} \\
\\
a&=\pm \frac{2\sqrt{3}}{3}
\end{align}
であり、 $~0 \le a < 4~$ から、 $~\displaystyle a=\frac{2\sqrt{3}}{3} ~$ 。
③ $~a \ge 4~$ のとき
\begin{align}
4a^2-8a+13&=1 \\
4a^2-8a+12&=0 \\
a^2-2a+3 &=0 \\
\end{align}
であり、この二次方程式は $~D < 0~$ となるため実数解はない。
以上①~③より、 $~\displaystyle a=-1,\frac{2\sqrt{3}}{3}~$ が求まった。
また、 $~a=-1~$ のときの最大値は、グラフから $~x=4~$ のとき。
$~f(x)~$ に $~a=-1,x=4~$ を代入して、
\begin{align}
&4^2-2\cdot(-1)\cdot 4+4\cdot(-1)^2-3 \\
&=16+8+4-3 \\
&=25
\end{align}
よって、最大値は $~25~$ となる。
次に、 $~\displaystyle a=\frac{2\sqrt{3}}{3}~$ のときの最大値を求める。
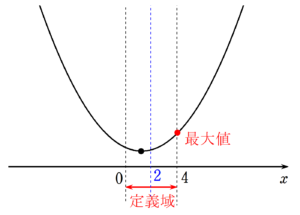
$~\displaystyle \frac{2\sqrt{3}}{3} < 2~$ より、グラフは次のようになる。
最大値は $~x=4~$ のときなので、 $~f(x)~$ に $~\displaystyle a=\frac{2\sqrt{3}}{3},x=4~$ を代入して、
\begin{align}
&\displaystyle 4^2-2\cdot \left( \frac{2\sqrt{3}}{3} \right) \cdot 4+4\cdot \left( \frac{2\sqrt{3}}{3} \right)^2-3 \\
\\
&=16-\frac{16\sqrt{3}}{3}+\frac{16}{3}-3 \\
\\
&=\frac{55}{3}-\frac{16\sqrt{3}}{3} \\
\\
&=\frac{55-16\sqrt{3}}{3} \\
\end{align}
\begin{align}
&\displaystyle 4^2-2\cdot \left( \frac{2\sqrt{3}}{3} \right) \cdot 4+4\cdot \left( \frac{2\sqrt{3}}{3} \right)^2-3 \\
\\
&=16-\frac{16\sqrt{3}}{3}+\frac{16}{3}-3 \\
\\
&=\frac{55}{3}-\frac{16\sqrt{3}}{3} \\
\\
&=\frac{55-16\sqrt{3}}{3} \\
\end{align}
よって、最大値は $~\displaystyle \frac{55-16\sqrt{3}}{3}~$ となる。
以上より、
\begin{cases}
a=-1のとき、&最大値は25(x=4) \\
\displaystyle a=\frac{2\sqrt{3}}{3}のとき、&最大値は\displaystyle \frac{55-16\sqrt{3}}{3}(x=4)
\end{cases}
\begin{cases}
&a=-1のとき、最大値は25(x=4) \\
\\
&\displaystyle a=\frac{2\sqrt{3}}{3}のとき、 \\
&最大値は\displaystyle \frac{55-16\sqrt{3}}{3}(x=4) \\
\end{cases}
この大問は数Ⅰ教科書レベルの問題。ここは確実に正答しておきたいところ。

◇参考文献等
・『私学教員適性検査問題集 数学(平成29年度~31年度)』
コメント