私学適性（数学）平成30年度解説　大問４

他の年度については、コチラからどうぞ。

　サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
　解説の内容自体に影響はありません。

---

問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。

---

４(1)

$~G~$ は重心なので、
\begin{align}
\overrightarrow{OG}&=\displaystyle \frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB} \\
\\
&=\frac{1}{3}\vec{a}+\frac{1}{3}\vec{b} \\
\\
&=\frac{1}{3}(\vec{a}+\vec{b})
\end{align}
が求まった。

---

４(2)

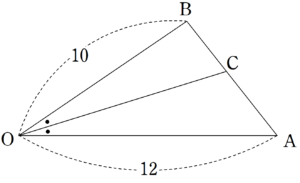
内角二等分線の性質より、
\begin{equation}
AC:CB=OA:OB=6:5
\end{equation}
なので、
\begin{align}
\displaystyle \overrightarrow{AC}&=\frac{6}{11}\overrightarrow{AB} \\
\\
&=\frac{6}{11}(\vec{b}-\vec{a})
\end{align}
が求まった。

---

４(3)

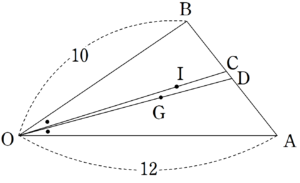
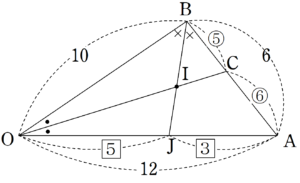
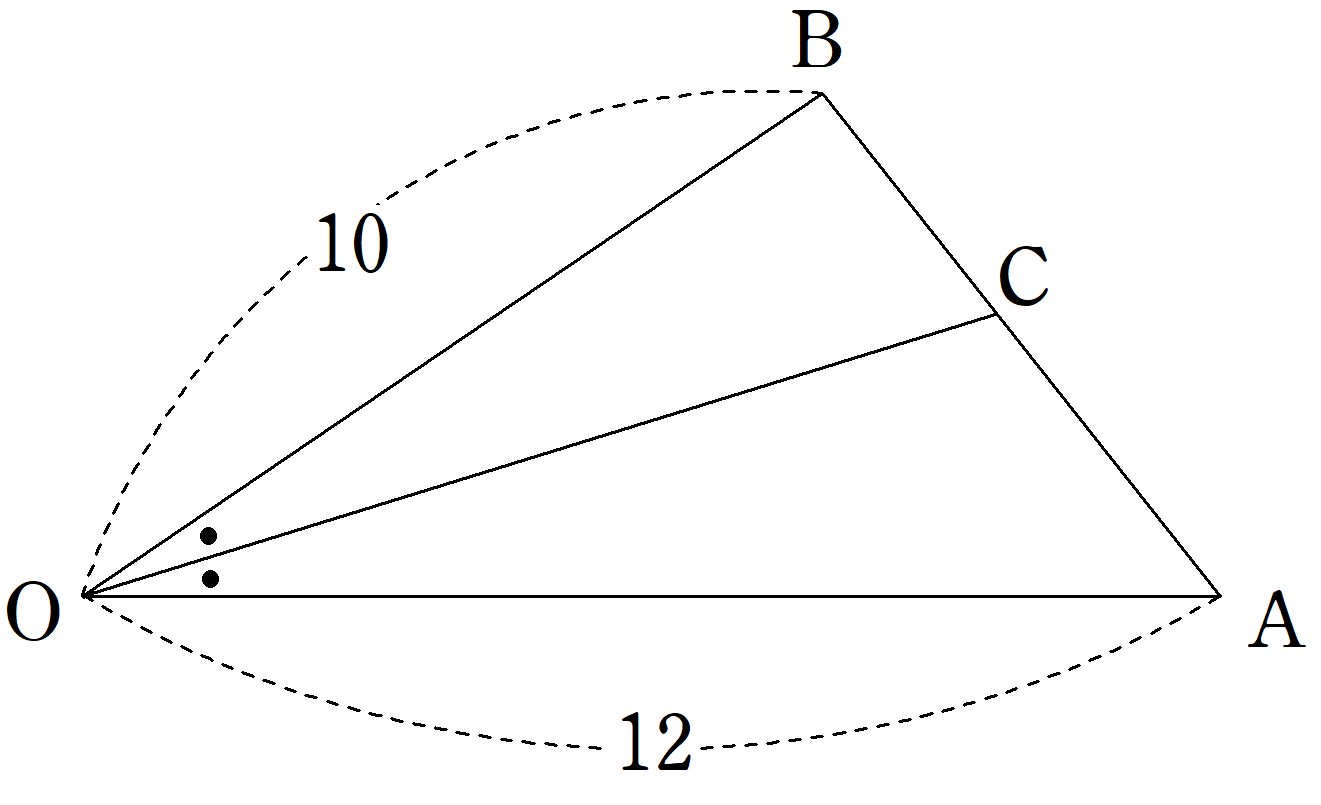
$~D~$ を $~AB~$ の中点とすると、次のような図になる。

$~\overrightarrow{GI}~$ を次のように分解する。
\begin{equation}
\overrightarrow{GI}=\overrightarrow{GD}+\overrightarrow{DC}+\overrightarrow{CI} \cdots (*)
\end{equation}
 
① $~\overrightarrow{GD}~$ を求める。
$~G~$ は重心なので、 $~OG:GD=2:1~$ となる。(1)より、
\begin{align}
\overrightarrow{GD}&=\displaystyle \frac{1}{2}\overrightarrow{OG} \\
\\
&=\frac{1}{2}\cdot \frac{1}{3}(\vec{a}+\vec{b}) \\
\\
&=\frac{1}{6}\vec{a}+\frac{1}{6}\vec{b}
\end{align}
が求まる。
 
② $~\overrightarrow{DC}~$ を求める。
辺 $~AB~$ に注目する。
(2)より、
\begin{equation}
AC:CB=6:5
\end{equation}
であり、また $~D~$ が $~AB~$ の中点なので、
\begin{equation}
AD:DB=1:1
\end{equation}
である。

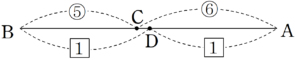
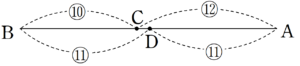
２種類の比を合わせることで、下のような比になる。

よって、
\begin{align}
\overrightarrow{DC}&=\displaystyle \frac{1}{22}\overrightarrow{AB} \\
\\
&=\frac{1}{22}(\vec{b}-\vec{a}) \\
\\
&=-\frac{1}{22}\vec{a}+\frac{1}{22}\vec{b}
\end{align}
が求まる。
 
③ $~\overrightarrow{CI}~$ を求める。
直線 $~BI~$ と $~OA~$ の交点を $~J~$ とすると、内角二等分線の性質から、
\begin{equation}
OJ:JA=BO:BA=5:3
\end{equation}
である。

ここで、メネラウスの定理より、
\begin{align}
\displaystyle \frac{OI}{IC}\cdot \frac{CB}{BA}\cdot \frac{AJ}{JO}&=1 \\
\\
\frac{OI}{IC}\cdot \frac{5}{11}\cdot \frac{3}{5}&=1 \\
\\
\frac{OI}{IC}&=\frac{11}{3}
\end{align}
となるため、 $~OI:IC=11:3~$ であることがわかる。
 
また、 $~C~$ は $~AB~$ を $~6:5~$ に内分する点であったので、
\begin{equation}
\overrightarrow{OC}=\displaystyle \frac{5}{11}\vec{a}+\frac{6}{11}\vec{b}
\end{equation}
である。
 
以上より、
\begin{align}
\overrightarrow{CI}&=\displaystyle \frac{3}{14}\overrightarrow{CO} \\
\\
&=-\frac{3}{14}\overrightarrow{OC} \\
\\
&=-\frac{3}{14} \left(\frac{5}{11}\vec{a}+\frac{6}{11}\vec{b} \right) \\
\\
&=-\frac{15}{154}\vec{a}-\frac{9}{77}\vec{b}
\end{align}
が求まる。
 
 
①～③を$(*)$に代入して、

\begin{align}
\overrightarrow{GI}&=\displaystyle \frac{1}{6}\vec{a}+\frac{1}{6}\vec{b}-\frac{1}{22}\vec{a}+\frac{1}{22}\vec{b}-\frac{15}{154}\vec{a}-\frac{9}{77}\vec{b} \\
\\
&=\frac{77}{462}\vec{a}+\frac{77}{462}\vec{b}-\frac{21}{462}\vec{a}+\frac{21}{462}\vec{b}-\frac{45}{462}\vec{a}-\frac{54}{462}\vec{b} \\
\\
&=\frac{11}{462}\vec{a}+\frac{44}{462}\vec{b} \\
\\
&=\frac{1}{42}\vec{a}+\frac{4}{42}\vec{b} \\
\\
&=\frac{1}{42}(\vec{a}+4\vec{b})
\end{align}

\begin{align}
\overrightarrow{GI}&=\displaystyle \frac{1}{6}\vec{a}+\frac{1}{6}\vec{b}-\frac{1}{22}\vec{a}+\frac{1}{22}\vec{b} \\
&-\frac{15}{154}\vec{a}-\frac{9}{77}\vec{b} \\
\\
&=\frac{77}{462}\vec{a}+\frac{77}{462}\vec{b}-\frac{21}{462}\vec{a}+\frac{21}{462}\vec{b} \\
&-\frac{45}{462}\vec{a}-\frac{54}{462}\vec{b} \\
\\
&=\frac{11}{462}\vec{a}+\frac{44}{462}\vec{b} \\
\\
&=\frac{1}{42}\vec{a}+\frac{4}{42}\vec{b} \\
\\
&=\frac{1}{42}(\vec{a}+4\vec{b})
\end{align}

が求まった。

---

---

◇参考文献等
・『私学教員適性検査問題集　数学（平成29年度～31年度）』