私学適性（数学）平成30年度解説　大問２

他の年度については、コチラからどうぞ。

　サイトのデザイン変更中に伴い、このページは多少見づらくなっています。 解説の内容自体に影響はありません。

---

問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。

---

２(1)

与式の左辺を因数分解していく。
\begin{align}
x^3-3x^2+(m+2)x-2m&=0 \\
x^3-3x^2+mx+2x-2m&=0 \\
x(x^2-3x+2)+(x-2)m&=0 \\
x(x-2)(x-1)+(x-2)m&=0 \\
(x-2)\{ x(x-1)+m \}&=0 \\
(x-2)(x^2-x+m)&=0 \\
\end{align}
これにより、解の１つは $~x=2~$ とわかったため、次のように場合分けして考える。

①　 $~x^2-x+m=0~$ が $~x=2~$ を解に持つ場合
$~x=2~$ を代入して、
\begin{align}
2^2-2+m&=0 \\
2+m&=0 \\
m&=-2
\end{align}
と求まる。このとき、
\begin{align}
x^2-x-2&=0 \\
(x-2)(x+1)&=0 \\
x&=2,-1
\end{align}
であるため、３重解にはならないことが確かめられた。

②　 $~x^2-x+m=0~$ が $~x=2~$ 以外の重解となる場合
判別式 $~D~$ を使うと、
\begin{align}
(-1)^2-4\cdot 1 \cdot m&=0 \\
1-4m&=0 \\
\\
m&=\displaystyle \frac{1}{4}
\end{align}
と求まる。このとき、
\begin{align}
\displaystyle x^2-x+\frac{1}{4}&=0 \\
\\
4x^2-4x+1&=0 \\
(2x-1)^2&=0 \\
x&=\frac{1}{2}(\neq 2)
\end{align}
であるため、３重解にはならないことが確かめられた。

以上①、②より、
\begin{equation}
\displaystyle m=-2,\frac{1}{4}
\end{equation}
が求まった。

　※この解法は、しなさんにご指南いただきました。ありがとうございました。

[wpex more=”ちなみにグラフで考えると・・・” less=”別解を閉じる”]
別解
$~y=x^3-3x^2+(m+2)x-2m~$ のグラフは、下の２つの図のどちらかとなる。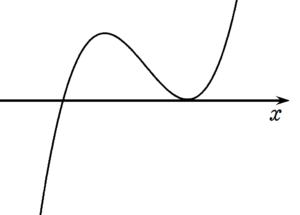


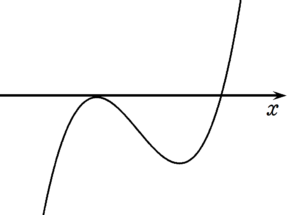
すなわち、 $~y’=0~$ を満たす $~x~$ が、 $~y=0~$ も満たすことになる。

まず、 $~y’=0~$ を満たす $~x~$ を求めると、
\begin{equation}
y’=3x^2-6x+(m+2)=0 \cdots ①
\end{equation}
より、解の公式を使うことで、
\begin{align}
x&=\displaystyle \frac{3 \pm \sqrt{9-3(m+2)}}{3} \\
\\
&=\frac{3 \pm \sqrt{3-3m}}{3} \\
\\
&=1 \pm \frac{\sqrt{3-3m}}{3} \cdots ②
\end{align}
がわかる。

ここで、①より、
\begin{equation}
3x^2=6x-m-2
\end{equation}
なので、次の２つの式が成り立つ。
\begin{align}
x^2&=2x-\frac{1}{3}m-\frac{2}{3} \cdots ③\\
\\
x^3&=\displaystyle 2x^2-\frac{1}{3}mx-\frac{2}{3}x \cdots ④\\
\end{align}

$~y=0~$ の式を、④と③を使って次数下げを行うと、

\begin{align}
x^3-3x^2+(m+2)x-2m&=0 \\
\\
\displaystyle 2x^2-\frac{1}{3}mx-\frac{2}{3}x-3x^2+mx+2x-2m&=0　　\\
\\
-x^2+\frac{2}{3}x+\frac{4}{3}x-2m&=0 \\
\\
-\left( 2x-\frac{1}{3}m-\frac{2}{3} \right) +\frac{2}{3}x+\frac{4}{3}x-2m&=0 \\
\\
-\frac{2}{3}x-\frac{5}{3}m+\frac{2}{3}mx+\frac{2}{3}&=0 \\
\\
2mx-2x-5m+2&=0 \\
\\
(2m-2)x-5m+2&=0
\end{align}

\begin{align}
x^3-3x^2+(m+2)x-2m&=0 \\
\\
\displaystyle 2x^2-\frac{1}{3}mx-\frac{2}{3}x-3x^2+mx+2x-2m&=0　　\\
\\
-x^2+\frac{2}{3}x+\frac{4}{3}x-2m&=0 \\
\\
-\left( 2x-\frac{1}{3}m-\frac{2}{3} \right) +\frac{2}{3}x+\frac{4}{3}x-2m&=0 \\
\\
-\frac{2}{3}x-\frac{5}{3}m+\frac{2}{3}mx+\frac{2}{3}&=0 \\
\\
2mx-2x-5m+2&=0 \\
\\
(2m-2)x-5m+2&=0
\end{align}

と $~x~$ の一次式に整理できる。

ここで、②を代入すると、

\begin{align}
\displaystyle (2m-2)\left(1 \pm \frac{\sqrt{3-3m}}{3} \right)-5m+2&=0 \\
\\
2m-2 \pm (2m-2)\cdot \frac{\sqrt{3-3m}}{3}&=5m-2 \\
\\
\pm (2m-2)\cdot \frac{\sqrt{3-3m}}{3}&=3m \\
\\
\pm (2m-2)\cdot \sqrt{3-3m}&=9m \\
\end{align}

\begin{align}
\displaystyle (2m-2)\left(1 \pm \frac{\sqrt{3-3m}}{3} \right)-5m+2&=0 \\
\\
2m-2 \pm (2m-2)\cdot \frac{\sqrt{3-3m}}{3}&=5m-2 \\
\\
\pm (2m-2)\cdot \frac{\sqrt{3-3m}}{3}&=3m \\
\\
\pm (2m-2)\cdot \sqrt{3-3m}&=9m \\
\end{align}

となり、両辺２乗すると、

\begin{align}
(2m-2)^2(3-3m)&=81m^2 \\
(4m^2-8m+4)(1-m)&=27m^2 \\
4m^2-8m+4-4m^3+8m^2-4m&=27m^2 \\
-4m^3+12m^2-12m+4&=27m^2 \\
-4m^3-15m^2-12m+4&=0 \\
4m^3+15m^2+12m-4&=0 \\
(m+2)(4m^2+7m-2)&=0 \\
(m+2)(m+2)(4m-1)&=0 \\
(m+2)^2(4m-1)&=0 \\
\end{align}

\begin{align}
(2m-2)^2(3-3m)&=81m^2 \\
(4m^2-8m+4)(1-m)&=27m^2 \\
4m^2-8m+4-4m^3+8m^2-4m&=27m^2 \\
-4m^3+12m^2-12m+4&=27m^2 \\
-4m^3-15m^2-12m+4&=0 \\
4m^3+15m^2+12m-4&=0 \\
(m+2)(4m^2+7m-2)&=0 \\
(m+2)(m+2)(4m-1)&=0 \\
(m+2)^2(4m-1)&=0 \\
\end{align}

と式変形できるので、
\begin{equation}
m=\displaystyle -2 ,\frac{1}{4}
\end{equation}
が求まった。

　さすがに面倒・・・。自分の中では、この方法しか思いつきませんでした・・・。

[/wpex]

---

２(2)

$~f(x)~$ を $~x+1~$ で割った余りは $~-4~$ なので、商を $~A(x)~$ とすると、
\begin{equation}
f(x)=(x+1)A(x)-4
\end{equation}
と表せる。よって
\begin{equation}
f(-1)=-4 \cdots ①
\end{equation}

同様に、 $~f(x)~$ を $~x-3~$ で割った余りは $~4~$ なので、商を $~B(x)~$ とすると、
\begin{equation}
f(x)=(x-3)B(x)+4
\end{equation}
と表せる。よって
\begin{equation}
f(3)=4 \cdots ②
\end{equation}

次に、 $~f(x)~$ を $~(x+1)(x-3)~$ で割ることを考えると、２次式で割るために余りは一次式である。よって、余りは $~ax+b~$ で表せる。商を $~C(x)~$ とすると、
\begin{equation}
f(x)=(x+1)(x-3)C(x)+ax+b
\end{equation}
と表せる。この式に①と②をそれぞれ代入すると、
\begin{cases}
f(-1)=-a+b = -4 & \\
f(3)=3a+b = 4 &
\end{cases}
であり、この連立方程式を解くと、 $~a=2,b=-2~$ である。

よって、余りは $~2x-2~$ と求まった。

---

２(3)

まず、 $~\alpha~$ を式変形していく。
\begin{align}
\alpha&=\sqrt{3}-i \\
\\
&=\displaystyle 2 \left( \frac{\sqrt{3}}{2}-\frac{1}{2}i \right) \\
\\
&=2\left\{ \cos{\left( -\frac{\pi}{6} \right)}+i \sin{\left( -\frac{\pi}{6} \right)} \right\} \\
\end{align}
両辺 $~n~$ 乗して、ド・モアブルの定理を適用すると、
\begin{equation}
\alpha^n=\displaystyle 2^n \left\{ \cos{\left( -\frac{\pi}{6}n \right)}+i \sin{\left( -\frac{\pi}{6}n \right)} \right\}
\end{equation}
となる。

$~\alpha^n~$ が整数となるためには、まず $~\sin{}~$ の部分（虚数部分）が $~0~$ にならなければいけない。それを満たす最小の自然数 $~n~$ は、
\begin{equation}
\displaystyle \sin{\left( -\frac{\pi}{6}\cdot 6 \right)}=\sin{(-\pi)}=0
\end{equation}
より、 $~n=6~$ 。このとき、 $~\alpha^6~$ の値は、
\begin{align}
\alpha^6&=\displaystyle 2^6 \left\{ \cos{(-\pi)}+i \cdot 0 \right\} \\
&=64 \cdot (-1) \\
&=-64
\end{align}
と整数になるため、 $~n=6~$ が求まった。

---

２(4)

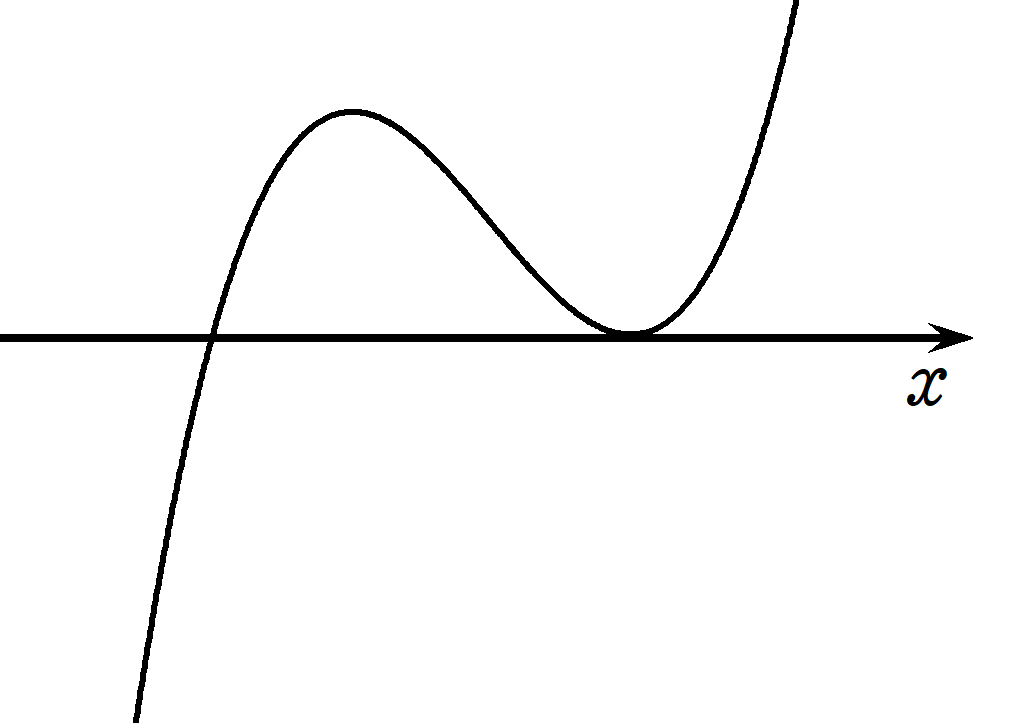
$~x^2+ax+b > 0~$ の解がすべての実数となるため、 $~y=x^2+ax+b~$ のグラフが次のような形になる。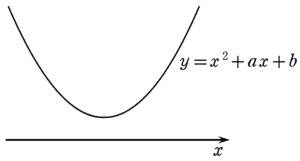

すなわち、判別式が $~D < 0~$ になるため、
\begin{align}
D=a^2-4b &< 0 \\
a^2 &< 4b
\end{align}
を満たす $~(a,b)~$ の組み合わせを見つければよい。

下の表から、条件を満たすのは $~17~$ 通りであるため、確率は $~\displaystyle \frac{17}{36}~$ と求まった。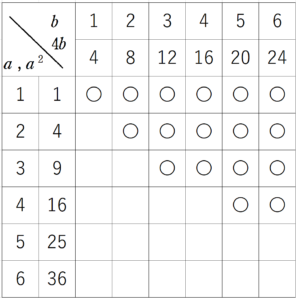

---

２(5)

$~24~$ の倍数なので、 $~24a~$ と表す。これを素因数分解すると、
\begin{equation}
24a=2^3 \cdot 3 \cdot a
\end{equation}
であり、この正の約数の個数が $~21(=1 \times 21,3 \times 7)~$ 個であることを考える。

「約数の個数」から、 $~2^3 \cdot 3 \cdot a~$ の指数の組み合わせは、 $~0~$ と $~20~$ または $~2~$ と $~6~$ となる。

しかし、すでに素因数 $~2~$ と $~3~$ があるため、 $~0~$ と $~20~$ の組み合わせは不適。

また、すでに $~2^3~$ が存在しているため、 $~24a=2^2 \cdot 3^6~$ も不適。

したがって、
\begin{align}
24a&=2^6 \cdot 3^2 \\
&=64 \cdot 9 \\
&=576
\end{align}
が求まった。

---

２(6)

$~2017 ^div 2=1008 \cdot 1~$ より、 $~2017~$ は $~1009~$ 番目の奇数である。

$~n~$ 群には奇数が $~n~$ 個入るので、 $~n~$ 群までに入っている奇数の個数を $~S_n~$ とすると、
\begin{align}
S_n&=1+2+3+\cdots+n \\
\\
&=\displaystyle \sum_{k=1}^{n} k \\
\\
&=\frac{n(n+1)}{2}
\end{align}
となる。

以上より、 $~S_{n-1} < 1009 \le S_{n}~$ を満たす自然数 $~n~$ を求めればよい。
\begin{align}
\displaystyle \frac{(n-1)n}{2} &< 1009 \le \frac{n(n+1)}{2} \\
\\
(n-1)n &< 2018 \le n(n+1) \\
\end{align}
この不等式を満たす自然数 $~n~$ は $~45~$ （ $~1980 < 2018 \le 2070~$ ）

よって、 $~45~$ 群であることが求まった。

　あてはまる $~n~$ を探すのは大変そうに思えますが、「下1桁が5の自然数の２乗」より、 $~45^2=2025~$ であることを知っていたため、すぐに予想がつきました。

---

２(7)

与式を変形すると、
\begin{align}
&\displaystyle \sum_{n=1}^{\infty} \left( \frac{1}{3^n}+\frac{2}{5^n} \right) \\
\\
&=\sum_{n=1}^{\infty} \frac{1}{3^n}+ \sum_{n=1}^{\infty}\frac{2}{5^n}
\end{align}
となる。

第１項の無限級数は、初項 $~\displaystyle \frac{1}{3}~$ 、公比 $~\displaystyle \frac{1}{3}~$ であり、第２項は初項 $~\displaystyle \frac{2}{5}~$ 、公比 $~\displaystyle \frac{1}{5}~$ であるため、
\begin{align}
&=\displaystyle \frac{\frac{1}{3}}{1-\frac{1}{3}}+\frac{\frac{2}{5}}{1-\frac{1}{5}}　　\\
\\
&=\frac{\frac{1}{3}}{\frac{2}{3}}+\frac{\frac{2}{5}}{\frac{4}{5}} \\
\\
&=\frac{1}{2}+\frac{2}{4} \\
\\
&=1
\end{align}
と求まった。

---

２(8)

$~x < y < z ~$ より、
\begin{align}
2xyz&=x+3y+4z \\
&< z+3z+4z \\
&=8z
\end{align}
と変形できる。したがって、
\begin{align}
2xyz &< 8z \\
xy &< 4
\end{align}
であり、 $~(x,y)=(1,2),(1,3)~$ が求まる。

$~(x,y)=(1,2)~$ のとき
\begin{align}
2\cdot 1 \cdot 2 \cdot z&=1+3\cdot 2 +4z \\
4z&=7+4z \\
0&=7
\end{align}
となり、不適。

$~(x,y)=(1,3)~$ のとき
\begin{align}
2\cdot 1 \cdot 3 \cdot z&=1+3\cdot 3 +4z \\
6z&=10+4z \\
2z&=10 \\
z&=5
\end{align}
となり、 $~x < y < z ~$ を満たす。

よって、 $~(x,y,z)=(1,3,5)~$ が求まった。

---

２(9)

$~\vec{a}=(4+t,-t,2\sqrt{2})~$ より、
\begin{align}
|\vec{a}|&=\sqrt{(4+t)^2+(-t)^2+(2\sqrt{2})^2} \\
&=\sqrt{16+8t+t^2+t^2+8} \\
&=\sqrt{2t^2+8t+24}
\end{align}
である。

$~x~$ 軸の正の向きの単位ベクトルを $~\vec{b}=(1,0,0)~$ とすると、
\begin{align}
&|\vec{b}|=1 \\
\\
&\vec{a}\cdot \vec{b}=4+t
\end{align}
が求まる。

$~\vec{a}~$ と $~\vec{b}~$ がなす角は $~60^{\circ}~$ なので、以上の式を代入して計算すると、
\begin{align}
\vec{a}\cdot \vec{b}&=|\vec{a}||\vec{b}|\cos{60^{\circ}} \\
\\
\displaystyle 4+t&=\sqrt{2t^2+8t+24} \cdot 1 \cdot \frac{1}{2} \\
\\
8+2t&=\sqrt{2t^2+8t+24} \cdots ①\\
\end{align}
となり、両辺２乗して、
\begin{align}
64+32t+4t^2&=2t^2+8t+24 \\
2t^2+24t+40&=0 \\
t^2+12t+20&=0 \\
(t+2)(t+10)&=0 \\
t&=-2,-10
\end{align}
が求まる。

しかし、①より、 $~8+2t \ge 0~$ より、 $~t=-10~$ は不適。

よって、 $~t=-2~$ が求まった。

---

２(10)

求めたい直線を $~\ell~$ とする。

直線 $~5x-y=0~$ 上の点 $~A(1,5)~$ をとり、直線 $~x+3y=0~$ に関して $~A~$ と対称な点を $~B(a,b)~$ とする。
このとき、 $~B~$ は $~\ell~$ 上にあり、 $~AB~$ と直線 $~x+3y=0~$ の交点を $~C~$ とする。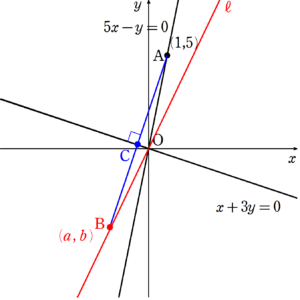

$~AB~$ の中点は $~\displaystyle \left( \frac{a+1}{2} , \frac{b+5}{2} \right)~$ と表せ、これが $~C~$ 、すなわち直線 $~x+3y=0~$ 上になるので、
\begin{align}
\displaystyle \frac{a+1}{2}+3\cdot \frac{b+5}{2}&=0 \\
\\
a+1+3b+15&=0 \\
\\
a+3b&=-16 \cdots ①
\end{align}

また、 $~AB~$ と直線 $~x+3y=0~$ は直交するので、
\begin{align}
\displaystyle \frac{5-b}{1-a} \cdot \left( -\frac{1}{3} \right)&=-1 \\
\\
5-b&=3(1-a) \\
\\
5-b&=3-3a \\
\\
3a-b&=-2
\end{align}
となる。

①と②を連立することで、 $~(a,b)=\displaystyle \left( -\frac{11}{5},-\frac{23}{5} \right)~$ が求まり、 $~\ell~$ はこの点と原点を通る直線であるため、
\begin{equation}
\displaystyle y=\frac{23}{11}x
\end{equation}
が求まった。

---

---

◇参考文献等
・『私学教員適性検査問題集　数学（平成29年度～31年度）』