私学適性（数学）平成30年度解説　大問１

他の年度については、コチラからどうぞ。

　サイトのデザイン変更中に伴い、このページは多少見づらくなっています。
　解説の内容自体に影響はありません。

---

問題集にも載っていますが、解答だけをまずは示します。
問題番号をクリックすると、各問題の解説にスクロールします。

---

１(1)

\begin{align}
&(x-1)(x+2)(x-3)(x+4) \\
&=\left\{(x-1)(x+2)\right\} \left\{(x-3)(x+4)\right\} \\
&=(x^2+x-2)(x^2+x-12) \\
\end{align}
ここで、 $~x^2+x=A~$ とおくと、
\begin{align}
&=(A-2)(A-12) \\
&=A^2-14A+24 \\
&=(x^2+x)^2-14(x^2+x)+24 \\
&=x^4+2x^3+x^2-14x^2-14x+24 \\
&=x^4+2x^3-13x^2-14x+24 \\
\end{align}
が求まった。

---

１(2)

\begin{align}
&\sqrt{7-\sqrt{48}} \\
&=\sqrt{7-2\sqrt{12}} \\
&=\sqrt{(2-\sqrt{3})^2} \\
\end{align}
$~2-\sqrt{3} \ge 0~$ より、
\begin{equation}
\sqrt{7-\sqrt{48}}=2-\sqrt{3}
\end{equation}
が求まった。

---

１(3)

それぞれの数を $~\log_{3}{X}~$ の形で表す。
 
\begin{align}
7&=7\log_{3}{3} \\
&=\log_{3}{3^7} \\
&=\log_{3}{2187}
\end{align}

\begin{align}
3\log_{3}{2}+\log_{3}{5}+1&=\log_{3}{2^3}+\log_{3}{5}+\log_{3}{3} \\
&=\log_{3}{(2^3 \times 5 \times 3)} \\
&=\log_{3}{120}
\end{align}

\begin{align}
&3\log_{3}{2}+\log_{3}{5}+1 \\
&=\log_{3}{2^3}+\log_{3}{5}+\log_{3}{3} \\
&=\log_{3}{(2^3 \times 5 \times 3)} \\
&=\log_{3}{120}
\end{align}

\begin{align}
4\log_{3}{4} &=\log_{3}{4^4} \\
&=\log_{3}{256} \\
\end{align}
 
底は $~3 > 1~$ であるため、真数を比較して、
\begin{equation}
3\log_{3}{2}+\log_{3}{5}+1 < 4\log_{3}{4} < 7
\end{equation}
が求まった。

---

１(4)

関数 $~x=3y^2-4y~$ を $~y~$ で微分すると、
\begin{equation}
\displaystyle \frac{dx}{dy}=6y-4
\end{equation}
である。
$~y \neq \displaystyle \frac{2}{3}~$ であることから、 $~6y-4 \neq 0~$ なので、両辺逆数をとって、
\begin{equation}
\displaystyle \frac{dy}{dx}=\frac{1}{6y-4}
\end{equation}
が求まった。

---

１(5)

部分積分法で計算していくと、

\begin{align}
&\displaystyle \int_{-2}^{2}(x+2)(x-2)^3dx \\
\\
&=\int_{-2}^{2}(x+2)\left\{ \frac{1}{4}(x-2)^4 \right\}’ dx \\
\\
&=\left[ (x+2) \frac{1}{4}(x-2)^4 \right]_{-2}^{2}-\int_{-2}^{2}\frac{1}{4}(x-2)^4dx \\
\\
&=0-\left[ \frac{1}{20}(x-2)^5 \right]_{-2}^{2} \\
\\
&=-\left( -\frac{1}{20}(-4)^5 \right) \\
\\
&=-\frac{256}{5}
\end{align}

\begin{align}
&\displaystyle \int_{-2}^{2}(x+2)(x-2)^3dx \\
\\
&=\int_{-2}^{2}(x+2)\left\{ \frac{1}{4}(x-2)^4 \right\}’ dx \\
\\
&=\left[ (x+2) \frac{1}{4}(x-2)^4 \right]_{-2}^{2} \\
&-\int_{-2}^{2}\frac{1}{4}(x-2)^4dx \\
\\
&=0-\left[ \frac{1}{20}(x-2)^5 \right]_{-2}^{2} \\
\\
&=-\left( -\frac{1}{20}(-4)^5 \right) \\
\\
&=-\frac{256}{5}
\end{align}

が求まった。

---

１(6)

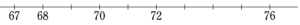
$~x~$ 点以外の５つの点数を数直線上に表すと、次のようになる。

$~x~$ 点を加えた６つの点数の中で、 $~x~$ の位置を次のように場合分けする。

①　２位以上のとき（72点以上）
②　単独３位のとき（71点）
③　３位タイのとき（70点）
④　単独４位のとき（69点）
⑤　５位以下のとき（68点以下）

①のとき、中央値は72点と70点の間にあるので、71点
 
②のとき、中央値は71点と70点の間にあるので、70.5点
 
③のとき、中央値は70点と70点の間にあるので、70点
 
④のとき、中央値は70点と69点の間にあるので、69.5点
 
⑤のとき、中央値は70点と68点の間にあるので、69点
 
以上より、 $~69点,69.5点,70点,70.5点,71点~$ が求まった。

---

１(7)

$~y=x^3+3x^2-3~$ を $~x~$ で微分すると、
\begin{equation}
y’=3x^2+6x
\end{equation}
となるため、 $~x=-2~$ における接線の傾きは、
\begin{equation}
3\cdot (-2)^2+6\cdot (-2)=0
\end{equation}
である。
 
よって、接線 $~y=0x+b~$ に $~(-2,1)~$ を代入して、 $~b=1~$ 。
したがって、直線 $~y=1~$ が接線となる。

---

１(8)

$~4^x-4^{-x}=3~$ の両辺を2乗して計算していく。
\begin{align}
(4^x-4^{-x})^2&=3^2 \\
4^{2x}-2\cdot 4^x \cdot 4^{-x}+4^{-2x}&=9 \\
4^{2x}-2+4^{-2x}&=9 \\
4^{2x}+4^{-2x}&=11 \cdots ①\\
\end{align}
 
次に、①を使って $~(4^x+4^{-x})^2~$ の値を考える。
\begin{align}
&(4^x+4^{-x})^2 \\
&=4^{2x}+2\cdot 4^x \cdot 4^{-x}+4^{-2x} \\
&=4^{2x}+4^{-2x}+2 \\
&=11+2 \\
&=13
\end{align}
ここで、 $~4^x > 0,4^{-x} > 0~$ より、 $~4^x+4^{-x} > 0~$ なので、
\begin{equation}
4^x+4^{-x}=\sqrt{13}
\end{equation}
が求まった。

---

１(9)

\begin{align}
\displaystyle r&=\frac{1}{\sin{\theta}+\cos{\theta}} \\
\\
r(\sin{\theta}+\cos{\theta})&=1 \\
\\
r\sin{\theta}+r\cos{\theta}&=1 \\
\end{align}
$~x=r\cos{\theta},y=r\sin{\theta}~$ なので、
\begin{equation}
x+y=1
\end{equation}
が求まった。

---

１(10)

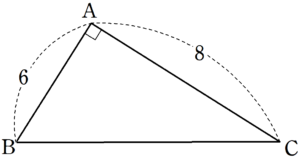
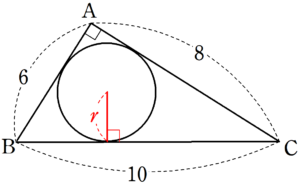
三平方の定理より、 $~BC=\sqrt{6^2+8^2}=10~$

$~\triangle ABC~$ の面積を２通りの方法で表すと、
\begin{align}
\triangle ABC&=\displaystyle \frac{1}{2}\cdot 6 \cdot 8=24 \\
\\
\triangle ABC&=\frac{r}{2}(6+8+10)=12r
\end{align}
であるため、 $~12r=24~$ より、 $~r=2~$ が求まった。

---

---

◇参考文献等
・『私学教員適性検査問題集　数学（平成29年度～31年度）』