現在の数学の源流の地とも言える古代ギリシャ。
論証数学が発展したこの地において、使われた数字は$~\alpha~$や$~\beta~$といったギリシャ文字でした。
単語を表す際にも使われたギリシャ文字が、数字としてどのように使われたのかをこの記事では解説します。
実は、数を記録するだけならまだしも、計算上は非常に不便な数字だったのです!
| 時代 | 紀元前8世紀頃~ |
| 場所 | ギリシャ |
アッティカ式とイオニア式
紀元前1050年頃に誕生したフェニキア文字から、ギリシャ文字(アルファベット)が生まれました。
紀元前8世紀半ば頃、ギリシャ文字は商業活動で用いられるようになったため、この時期に数字としても使われ始めたと考えられます。
古代ギリシャでは、2種類の記数法が存在していました。
地域によって数字の表し方が異なった
古代ギリシャの数字の表し方は、アテネを中心とするアッティカ地方で使われていた「アッティカ式」とミレトスやサモス島を含むイオニア地方で使われた「イオニア式」の2種類がありました。
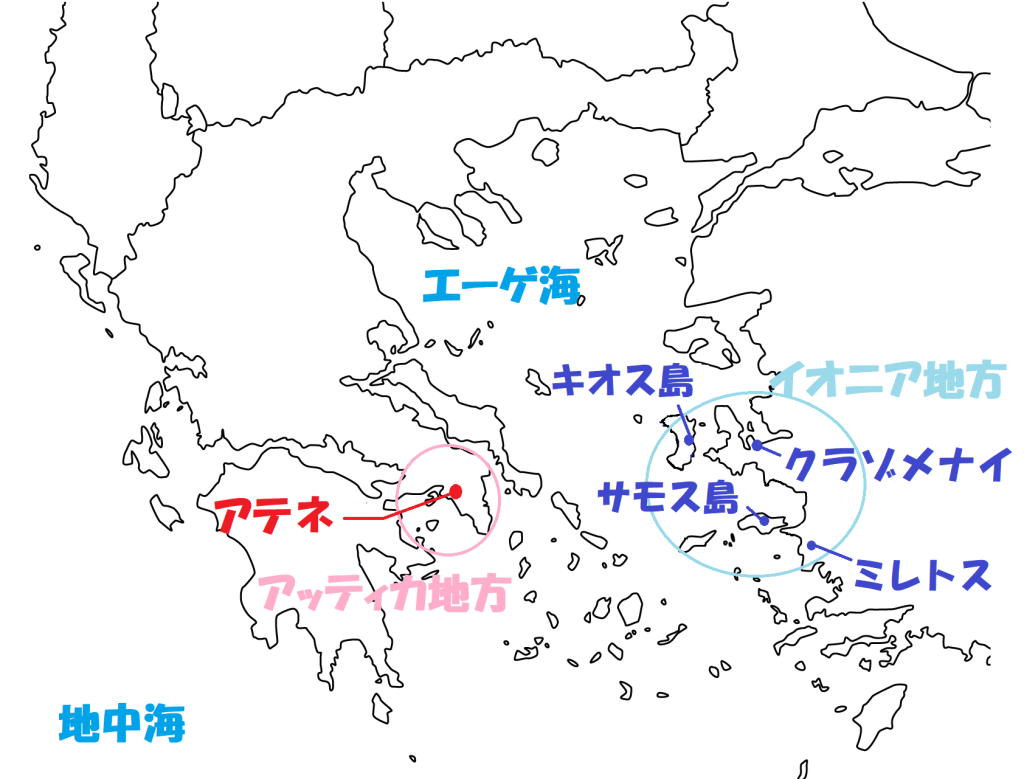
(出典:白地図専門店より改変 / CC-BY-4.0)
アテネの発展の発展に伴い、アッティカ式が先に誕生しました。
しかし、イオニア地方出身の数学者(下記参照)の影響や、イオニア式の使いやすさにより、紀元前5世紀頃にはアテネでもイオニア式が正式に使われるようになります。
- タレス(ミレトス出身)
- ピタゴラス(サモス島出身)
- アナクサゴラス(クラゾメナイ出身)
- ヒポクラテス(キオス出身)

(出典:Unidentified engraver, Public domain, via Wikimedia Commons)

(出典:The original uploader was Galilea at German Wikipedia., Public domain, via Wikimedia Commons)
アッティカ式は徐々に使われなくなり、逆にイオニア式は15世紀頃まで使われるくらい広まっていきました。
それぞれの数字の特徴を見ていきましょう。
アッティカ式の表し方
アテネ周辺で使われたアッティカ式ですが、記述するのが大変、表せる数に限界があるといった弱点がありました。
6種類を並べるだけ
用意された数字は、ギリシャ文字5種類と「1」のみ。
ギリシャ文字に関しては、ギリシャ語の数詞の頭文字を数字として採用していました。
| 数 | アッティカ式数字 | 由来となる数詞 |
| $1$ | | | (縦棒) |
| $5$ | $\Gamma$ | gente※1 |
| $10$ | $\Delta$ | deka |
| $100$ | $\Eta$ | hekaton |
| $1000$ | $\Chi$ | khilioi |
| $10000$ | $\Mu$ | myrioi |
※1 かつて、$~5~$を表す単語は”pente“だったため、$~\Pi~$を使うこともありました。
これらを並べることで、数を表すことができました。
- $~8~\cdots~\Gamma~$|||
- $~124~\cdots~\Eta~\Delta~\Delta~$||||
- $~23405~\cdots~\Mu~\Mu~\Chi~\Chi~\Chi~\Eta~\Eta~\Eta~\Eta~\Gamma~$
このように必要な数だけ数字を並べるという表し方は、古代エジプトのヒエログリフと同様であると言えるでしょう。

50や500は合字を使った
古代エジプトと違うのは、$~5~$を表す数字がある点。
さらに、$~5~$と既存の数字を組み合わせることで、新たな数字を作ることもできました。
| 数 | アッティカ式数字(合字) | 作り方 |
| $50$ | 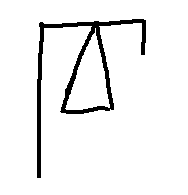 | $\Delta \times \Gamma~~(10\times5)$ |
| $500$ |  | $\Eta \times \Gamma~~(100\times5)$ |
| $5000$ |  | $\Chi \times \Gamma~~(1000\times5)$ |
| $50000$ |  | $\Mu \times \Gamma~~(10000\times5)$ |
この点を見れば、中国の甲骨文字と似ています。

しかし、大きな数を表す上では、書くのが大変であったり、書ける数に上限があったりという点が不便であったため、それらの問題点を解決したイオニア式に取って代わられていきました。
イオニア式の表し方
イオニア式は、アッティカ式よりも使う文字数が多い分、書くのが簡単な表し方となっています。
ギリシャ文字27種類を使用する
イオニア式では、ギリシャ文字全24種類に加え、さらに古い時代に使われていたギリシャ文字3種類(Ϝ、Ϙ、Ϡ)の計27種類を用いて表しました。
| 数 | イオニア式大文字 | イオニア式小文字 | 読み方 |
| $1$ | $\Alpha$ | $\alpha$ | alpha |
| $2$ | $\Beta$ | $\beta$ | beta |
| $3$ | $\Gamma$ | $\gamma$ | gamma |
| $4$ | $\Delta$ | $\delta$ | delta |
| $5$ | $\Epsilon$ | $\epsilon$ | epsilon |
| $6$ | Ϝ | ϝ | digamma |
| $7$ | $\Zeta$ | $\zeta$ | zeta |
| $8$ | $\Eta$ | $\eta$ | eta |
| $9$ | $\Theta$ | $\theta$ | theta |
| $10$ | $\Iota$ | $\iota$ | iota |
| $20$ | $\Kappa$ | $\kappa$ | kappa |
| $30$ | $\Lambda$ | $\lambda$ | lambda |
| $40$ | $\Mu$ | $\mu$ | mu |
| $50$ | $\Nu$ | $\nu$ | nu |
| $60$ | $\Xi$ | $\xi$ | xi |
| $70$ | $\Omicron$ | $\omicron$ | omicron |
| $80$ | $\Pi$ | $\pi$ | pi |
| $90$ | Ϙ | ϙ | koppa |
| $100$ | $\Rho$ | $\rho$ | rho |
| $200$ | $\Sigma$ | $\sigma$ | sigma |
| $300$ | $\Tau$ | $\tau$ | tau |
| $400$ | $\Upsilon$ | $\upsilon$ | upsilon |
| $500$ | $\Phi$ | $\phi$ | phi |
| $600$ | $\Chi$ | $\chi$ | chi |
| $700$ | $\Psi$ | $\psi$ | psi |
| $800$ | $\Omega$ | $\omega$ | omega |
| $900$ | Ϡ | ϡ | zampi |
最初は大文字だけだったものの、小文字の発明後は小文字が主に使われるようになりました。
これらの27種類の数字を使うことで、$~999~$までの数は最大でも3文字で表すことができます。
- $~37~\cdots~\lambda~\zeta~$
- $~66~\cdots~\xi~$ϝ
- $~281~\cdots~\sigma~\pi~\alpha~$
- $~809~\cdots~\omega~\theta~$
ちなみにですが、言葉と数字を区別する際には、数字の上に線を引きました。
英語で例えると、$~\bar{B}~Bananas~$(2本のバナナ)のようなイメージです。
1000以上は特別な記号や文字を使った
単に27文字を使うだけでは、$~999~$以下の数しか表すことができません。
そこで、$~1000~,~2000~,~\cdots~,~9000~$は、$~1~$から$~9~$を表す文字の前に、コンマ( ,)をつけることで表しました。
- $~1000~\cdots~,\alpha~$
- $~4000~\cdots~,\delta~$
- $~7777~\cdots~,\zeta ~\psi~\omicron~\zeta~$
- $~4003~\cdots~,\upsilon~\gamma~$
さらに$~10000~$以上を表す際には、$~10000~$倍したい数の前または下に”M”を付けます。
ギリシャ語で「無数」を表す”Muriado“の頭文字が由来です。
- $~10000=10000 \times 1~$$\cdots$$~M\alpha~$または$~\overset{\alpha}{M}~$
- $~12340000=10000 \times 1234~$$\cdots$$~M~,\alpha~\sigma~\lambda~\delta~$または$~\overset{,\alpha~\sigma~\lambda~\delta}{M}~$
- $~12000034=10000 \times 1200+34~$$\cdots$$~M~,\alpha~\sigma~\cdot~\lambda~\delta~$または$~\overset{,\alpha~\sigma}{M}\lambda~\delta~$
- $~120034=10000 \times 12+34~$$\cdots$$~M~\iota~\beta~\cdot~\lambda~\delta~$または$~\overset{\iota~\beta}{M}\lambda~\delta~$
- $~123400=10000 \times 12+3400~$$\cdots$$~M~\iota~\beta~\cdot~,\gamma~\upsilon~$または$~\overset{\iota~\beta}{M},\gamma~\upsilon~$
上記の例のように、”M”を前に置く場合には、$~10000~$倍する数としない数の境目に”・”を置いて区別しました。
バビロニア同様、位取りに近い考え方を持っていたことがわかります。

分数は単位分数のみで「´」をつけて表す
エジプト同様、実用性の観点から、ギリシャ人も単位分数を好みました。
単位分数は、分母となる数の後ろに、ダッシュ($~\prime~$)をつけることで表せます。
- $~\displaystyle \frac{1}{5}~$・・・・$~\epsilon^{\prime}~$
- $~\displaystyle \frac{1}{38}~$・・・・$~\lambda~\eta^{\prime}~$
- $~\displaystyle \frac{1}{1059}~$・・・・$~,\alpha \nu \theta^{\prime}~$
ただ、上の例の$~\displaystyle \frac{1}{38}~$や$~\displaystyle \frac{1}{1059}~$は、それぞれ$~\displaystyle 30\frac{1}{8}~$や$~\displaystyle 1050\frac{1}{9}~$との区別が無いため、前後の文脈から判断するという、これまたバビロニアの位取りのような曖昧さがありました。
まとめ・参考文献
古代ギリシャで使われた2種類の数字について解説しました。
- アッティカ式とイオニア式があったものの、長く使われたのはイオニア式。
- アッティカ式は古代エジプト同様、並べるだけの記数法。
- イオニア式はバビロニアのような位取りの考えが用いられた。
次の記事では、イオニア地方の数学者タレスについて紹介します。


アルファベットを数字として使っているけど、文章を読むときに混乱しなかったの?



文字と数字が混在するときには、数を表すアルファベットの上だけに線を引いて区別したんだ。



英語だけど、$~\bar{B}~Bananas~$(2本のバナナ)みたいなもんか~。
そんな工夫ができるんだったら、分数もどこまでが分母かわかりやすくして欲しかったな。
参考文献(本の紹介ページにリンクしています)
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,pp.55-58
- 『数学史 数学5000年の歩み』,pp.84-86
- 『ずかん 数字』,pp.60-61
- 『数学の流れ30講(上)』,pp.48-49


コメント