紀元前に誕生し、中国数学の体系を完成させた『九章算術』。
『九章算術』の9章「句股」で扱われている三平方の定理の問題では、二次方程式を利用するものも登場します。
特に、単なる開平法だけでは解けない二次方程式は幾何的に考え、二次方程式の解の公式に近い解き方をしていました。
この記事では、図を何枚も使いながら『九章算術』の二次方程式の解法を解説します。
| 時代 | B.C.2世紀頃~3世紀 |
| 場所 | 中国 |
古代中国の二次方程式
古代中国では、バビロニアほど細かくは研究されていないものの、二次方程式に関する記録が残っています。
『九章算術』9章で扱われた
『九章算術』は紀元前2世紀頃に書かれた、古代中国を代表する数学書です。

(出典:See page for author, Public domain, via Wikimedia Commons)
『九章算術』9章の「句股」では、三平方の定理に関する問題が全部で24題扱われています。
その24題のジャンルや難易度は様々ですが、各問題に適した術(公式や解法)が与えられたため、術にあてはめることで解を求めることができました。

9章の多くは単なる開平法や式変形で解ける問題
三平方の定理を利用するうえで、避けて通れないのは二次方程式ですが、『九章算術』9章の問題のほとんどは開平法や式変形だけで解くことができます。
開平法は『九章算術』4章で登場し、9章においては以下のような問題で使われました。
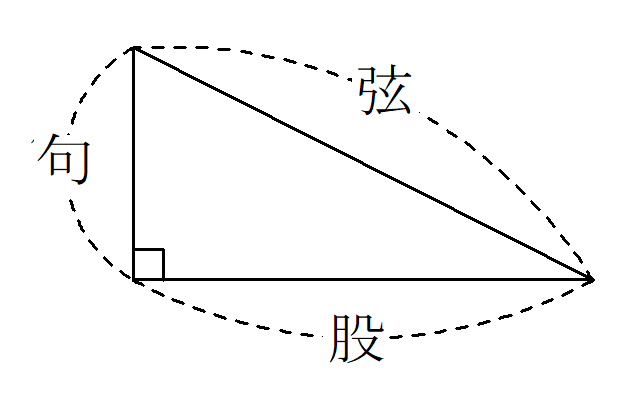
今、句が$~3~$尺※1、股が$~4~$尺の直角三角形がある。
弦の長さはいくらになるか。
※1「尺」は長さの単位で、当時は1尺=約23cmと推測されている。
この問題を、「句・股をそれぞれ自乗※2して、それらを足して開平術を使う」、すなわち
※2 「自乗」は2乗のこと。
弦=\sqrt{3^2+4^2}=5~(尺)という計算で解いていました。開平法さえ知っていれば解くことができます。
また、三平方の定理を利用するものの、解を出す上では二次方程式にならない問題もあります。
今$~1~$丈※3四方の池があり、葭が池の中央に生えていて、水から$~1~$尺出ている。
葭を岸まで引っ張ってくると、岸とちょうど等しくなる。
水深と葭の長さはそれぞれいくらか。
※3「丈」は長さの単位で、1丈=10尺。
この問題を現在の数学で考えると、水深を$~x~$尺として、
\begin{align*}
x^2+5^2&=(x+1)^2 \\
x^2+25&=x^2+2x+1 \\
-2x&=-24 \\
x&=12
\end{align*}となるため、実質一次方程式となります。
そのため、『九章算術』では与えられた公式を使うことで、
\begin{align*}
水深&=\frac{5^2-1^2}{2\cdot 1} \\
\\
&=\frac{24}{2} \\
\\
&=12 ~(尺) \\
\\
葭&=12+1 \\
&=13~(尺)
\end{align*}と求まり、原理的には単なる式変形だけで解が出ています。
しかし、『九章算術』の中には、開平法や式変形では解けないものもありました。
通常の開平法では解けない二次方程式の解法
通常の開平法では解けない二次方程式というのは、$~x^2-3x+2=0~$のように$~x~$の係数が$~0~$ではないものです。
通常の開平法では解けない問題は2つあった
『九章算術』の中で、$~x~$の係数が$~0~$ではない二次方程式を扱っていたのは、以下の2題です。
戸の高さが広※4より$~6~$尺$~8~$寸※5多く、対角の距離が$~1~$丈のものがある。
戸の高さと広はそれぞれいくらか。
※4「広」は横幅のこと。
※5「寸」は長さの単位で、100寸=10尺=1丈。
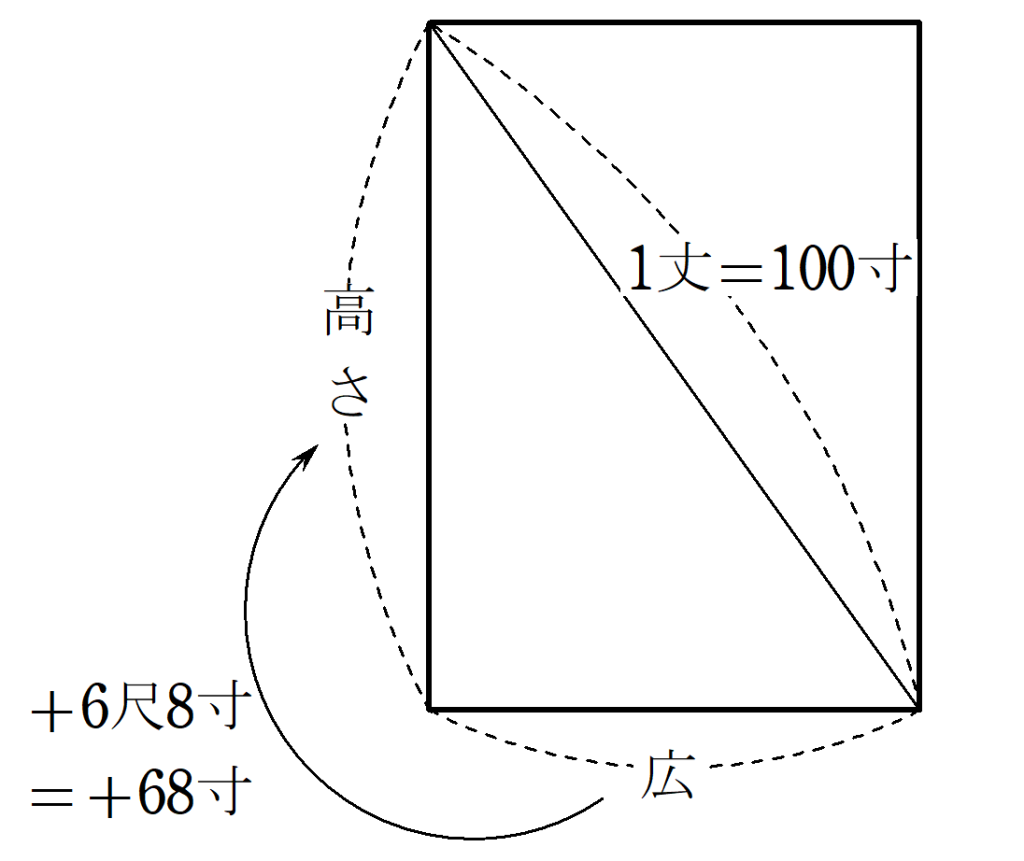
現代数学で考えると、広を$~x~$寸として、
\begin{align*}
x^2+(x+68)^2&=100^2 \\
x^2+x^2+136x+4624&=10000 \\
2x^2+136x-5376&=0 \\
x^2+68x-2688&=0 ~~~\cdots①\\
(x-28)(x+96)&=0 \\
x&=28
\end{align*}と求めることになります。
正方形の邑があり、各辺の真ん中に門を開いている。
北門を出て$~20~$歩のところに木がある。
南門を出て$~14~$歩のところで西を向き、さらに$~1775~$歩のところで木が見える。
邑の一辺の長さはいくらか。
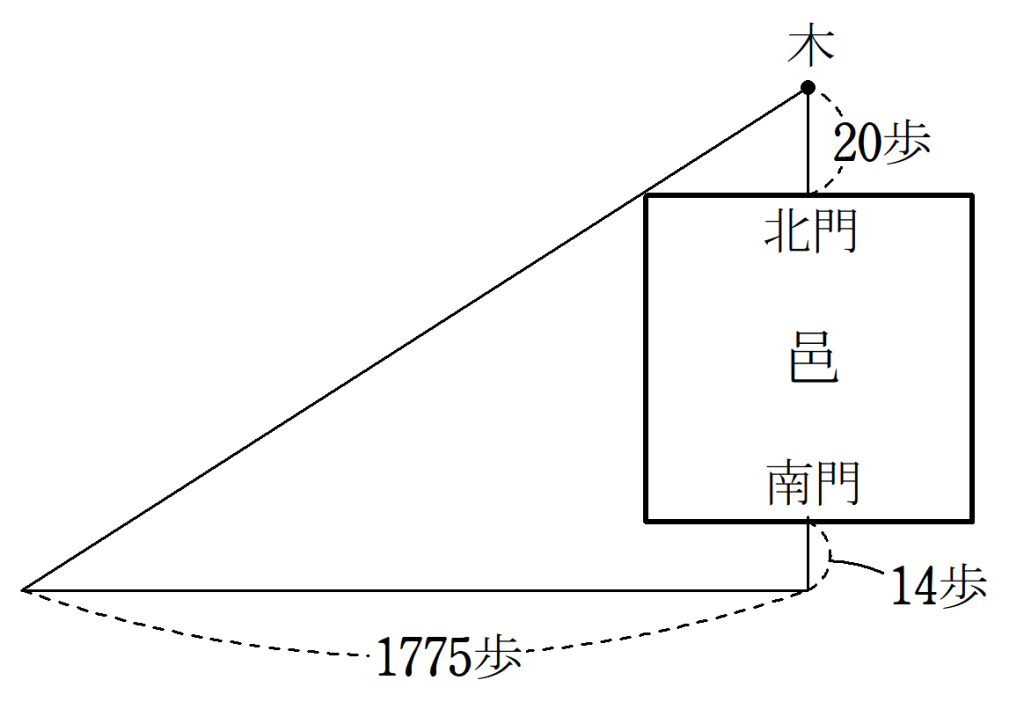
こちらも現代数学を使えば、邑の一辺を$~x~$歩として、
\begin{align*}
\frac{1}{2}x:20&=1775:(14+x+20) \\
\frac{1}{2}x^2+17x&=35500 \\
x^2+34x-71000&=0 ~~~\cdots②\\
(x-250)(x+284)&=0 \\
x&=250
\end{align*}と求めることができます。
(三平方の定理を使っていないものの、直角三角形に関する問題のため、9章「句股」で扱われています。)
2問とも、$~x~$の係数が$~0~$ではない二次方程式を使っているため、単なる開平法や式変形だけでは解けない問題といえます。
従法(1次の項の係数)を利用した特別な開平法
『九章算術』では、特別な開平法を用いて、二次方程式の解を求めました。
『九章算術』9章第11問 であれば、$①$の$~x^2+68x-2688=0~$から、以下のように計算しています。
\begin{align*}
x&=(\sqrt{2688\times 4+68^2}-68) \div 2 \\
&=(\sqrt{15376}-68) \div 2 \\
&=(124-68) \div 2 \\
&=28
\end{align*}同様に、『九章算術』9章第20問では、$②$の$~x^2+34x-71000=0~$から、
\begin{align*}
x&=(\sqrt{71000\times 4+34^2}-34) \div 2 \\
&=(\sqrt{285156}-34) \div 2 \\
&=(534-34) \div 2 \\
&=250
\end{align*}と計算されており、単なる開平法ではなく、決まった数値計算をしてからの開平法を利用していることがわかります。
『九章算術』では、$~x~$の係数のことを「従法」と呼んでいたため、この開平法のことを「帯従開平」と言います。
式の意味は解の公式
「帯従開平」を現代数学で紐解いてみましょう。
二次方程式$~x^2+bx-c=0~$の解は、次の式で与えられる。
x=\frac{-b+\sqrt{b^2+4c}}{2}「帯従開平」を用いた式の項の並び替えをしてみると、「帯従開平」は、現在の二次方程式の解の公式において$~a=1~$かつ負の解が出ないパターンであることがわかります。
古代中国では、算木によって負の数を計算で扱うことができたものの、負の数が答えとなることは無かったため、$~\pm~$ではなく、$~+~$のみとなっていました。
『九章算術』よりも1500年ほど古いバビロニアにおいても、この形の二次方程式は扱われています。

解法の原理は幾何的に理解されていた
現代数学であれば、解の公式は平方完成を利用して導かれますが、古代中国では幾何的に理解されました。
魏の数学者である劉徽が、263年に書いた『九章算術』の注釈本に、その説明が載っています。
劉徽の考え方に則して、「帯従開平」(現代数学版) を証明してみましょう。
二次方程式$~x^2+bx-c=0~$を、以下のように変形する。
\begin{align*}
x^2+bx&=c \\
x(x+b)&=c ~~~\cdots ③\\
\end{align*} 縦$~x~$、横$~x+b~$の長方形を考えると、$③$より、面積は$~c~$となる。
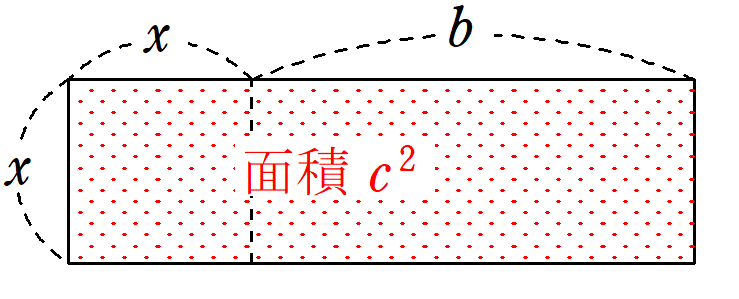
この長方形を4つ用いて、一辺が$~2x+b~$の正方形を作る。
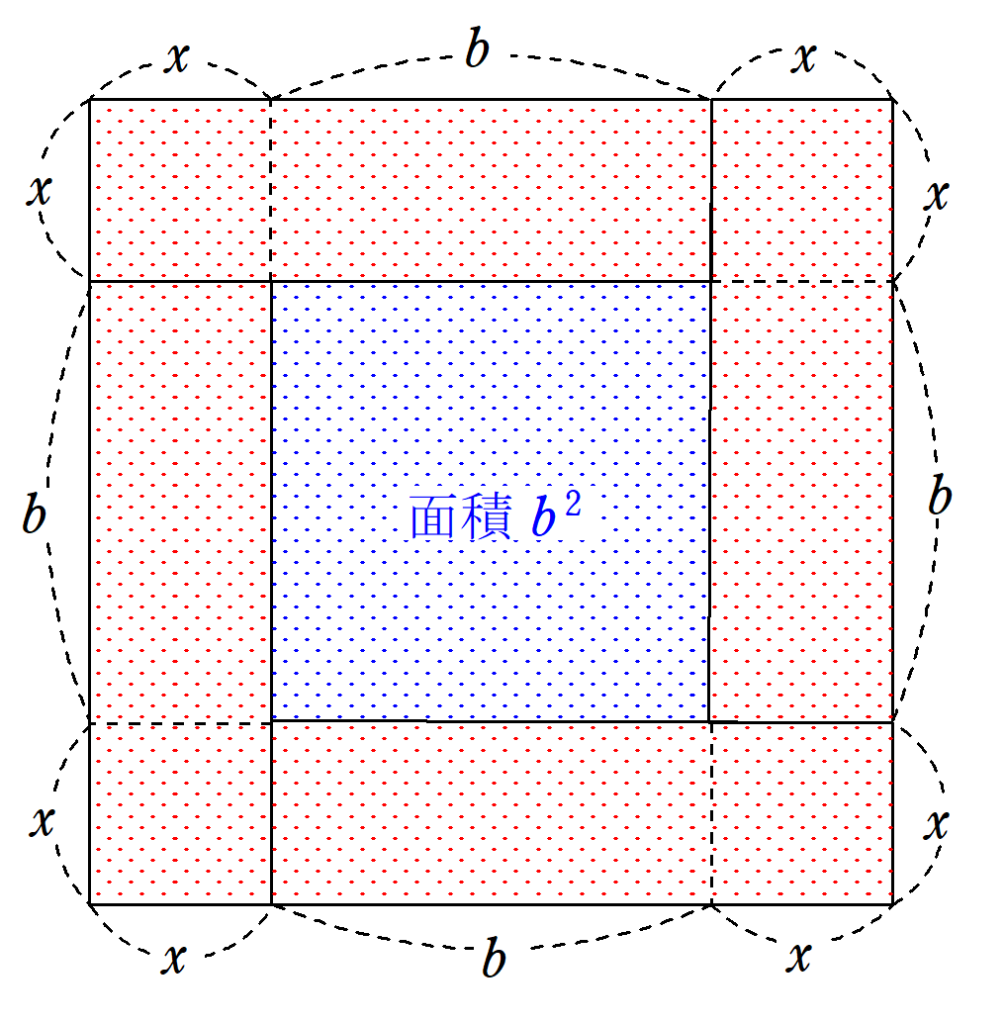
この正方形の面積は、$~b^2+4c~$であるため、開平算を使うことで、
2x+b=\sqrt{b^2+4c}~~~\cdots④が成り立つ。(一辺の長さなので、$~-\sqrt{b^2+4c}~$は不適)
$④$を$~x~$について解くことで、
\begin{align*}
2x&=-b+\sqrt{b^2+4c} \\
\\
x&=\frac{-b+\sqrt{b^2+4c}}{2}
\end{align*} が求まる。
元の『九章算術』(紀元前2世紀頃)には、ここまで詳しい説明が載っていませんでした。
劉徽が『九章算術』の術一つ一つにこのような証明を加えていったことから、B.C.200 ~ 263年の約400年の間に「証明」という文化がヨーロッパから中国に伝わったと考えられます。
まとめ・参考文献
古代中国における二次方程式について解説しました。
- 古代中国の数学書『九章算術』の9章では、二次方程式の解法を扱っている。
- 9章第11問と第20問では、解の公式を原理とした解法が載っている。
- 263年に劉徽が書いた注釈書では、二次方程式の解法を幾何的に解説している。
二次方程式自体は紀元前のバビロニアでも扱われていたものの、解法を幾何的に証明している点が古代中国の強みと言えるでしょう。
「証明」という文化は、古代ギリシャで生まれました。
次の章では、古代ギリシャの数学や数学者について解説します。



解の公式を覚えた方が遥かに楽だということがわかりました。



昔はパターンごとに解法が分かれていたから、覚えるのも一苦労だったろうね。
参考文献(本の紹介ページにリンクしています)
- 大川俊隆・田村誠「『九章算術』訳注稿(30)」,< https://osu.repo.nii.ac.jp/?action=pages_view_main&active_action=repository_view_main_item_detail&item_id=2016&item_no=1&page_id=13&block_id=21よりダウンロード>
- 田村誠「『九章算術』訳注稿(31)」,<https://osu.repo.nii.ac.jp/?action=pages_view_main&active_action=repository_view_main_item_detail&item_id=2069&item_no=1&page_id=13&block_id=21よりダウンロード>
- 『カッツ 数学の歴史』,pp.41-42
- 『メルツバッハ&ボイヤー 数学の歴史Ⅰ』,p.194
- 『数学史 数学5000年の歩み』,pp.135-137
- 『数学の歴史物語』,pp.167-183
- 『ずかん 数字』,pp.70-77

コメント