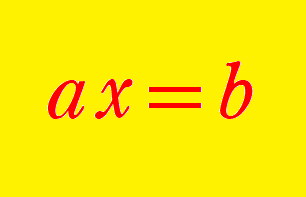-

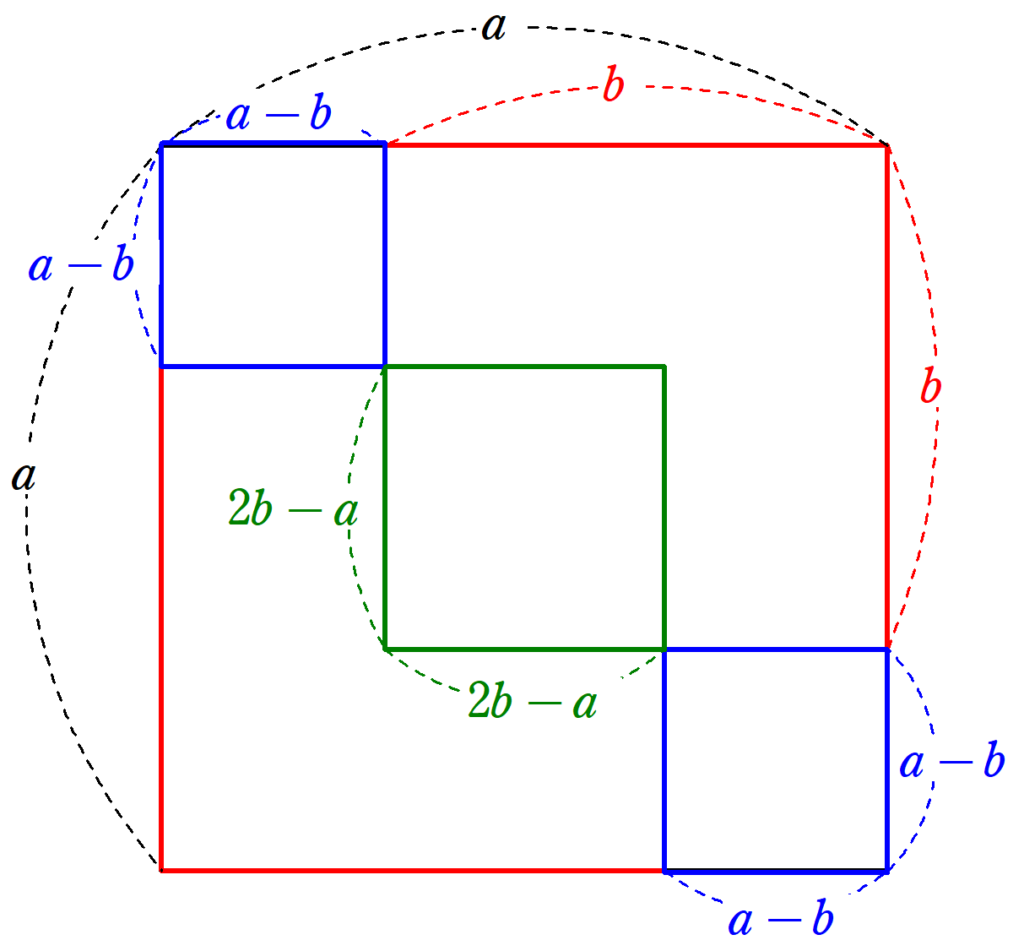
【有名問題】√2が無理数であることの証明~3種類の証明方法とは?~
古代ギリシャから考えられていたルート2 が無理数であることの証明。その歴史の深さと、実際の証明方法を3種類解説します。 -

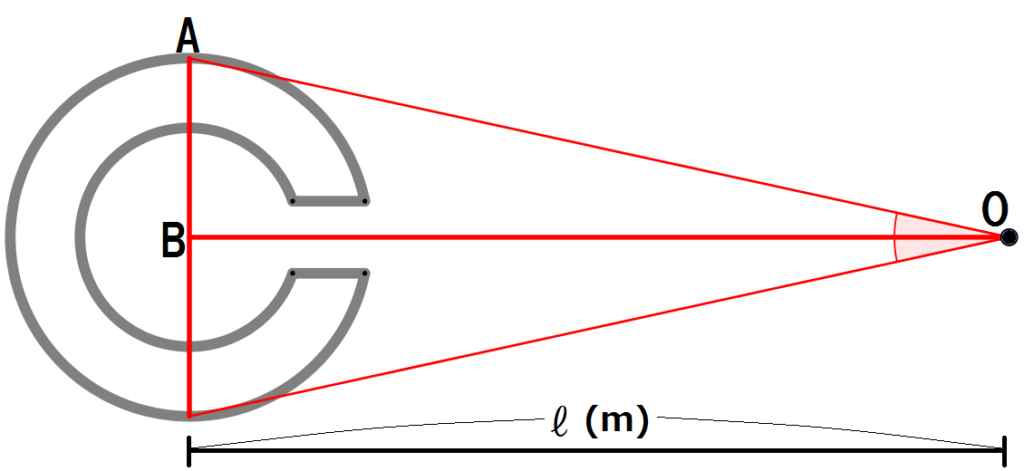
ランドルト環~視力検査のCの仕組みを数学で解説! 使われているのは反比例だった?~
視力検査で使われる「C」のことをランドルト環といいます。測りたい視力と距離に応じて、ランドルト環の大きさはどのように決まっているのかを解説します。 -

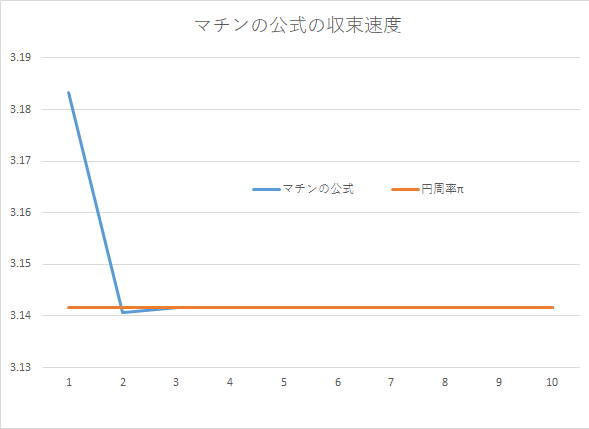
マチンの公式
1706年、イギリスのジョン・マチンによって示された公式です。非常に収束速度が速い級数が使われていて、円周率の $~\displaystyle \frac{1}{4}~$ の値を求めることがで... -

グレゴリー級数
1671年、スコットランドのジェームス・グレゴリーが発見した $~\tan^{-1}x~$ に関する級数です。この級数によって、円周率の近似値の研究が格段に進みました。グレゴリ... -

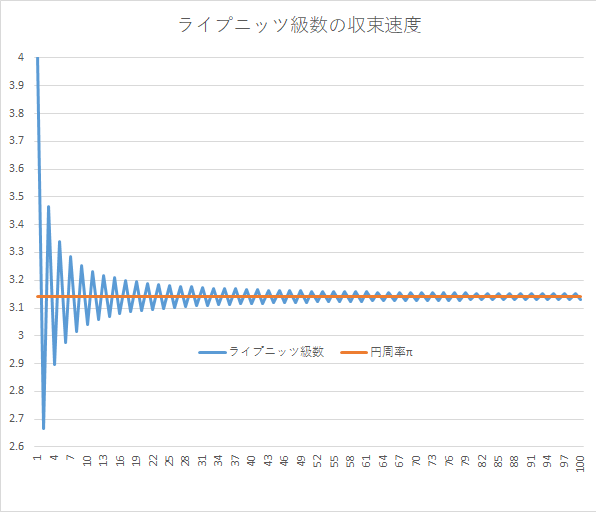
ライプニッツ級数
1674年、ゴットフリート・ライプニッツによって示された級数です。円周率の $~\displaystyle \frac{1}{4}~$ の値が単純な分数のたし算引き算によって表されます。17世紀... -

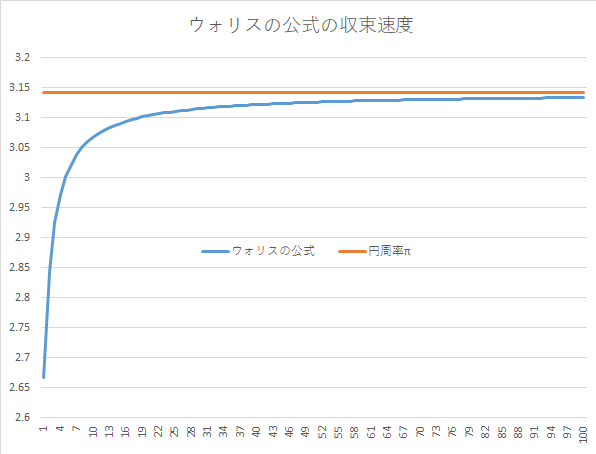
ウォリスの公式
イングランドの数学者ジョン・ウォリス(John Wallis)が、1656年に主著の中で発表した公式です。ある規則で並んだ分数を無限にかけていくと円周率が登場するため、微積... -

旧ISBNコードのしくみ
2007年1月から13ケタとなったISBNコード。その前に出版された書籍のISBNコードは10ケタでした。現行の13ケタと比較しながら、10ケタのISBNコード(ISBN-10)について説... -

ISBNコードのしくみ
本の背表紙にある13ケタの数字はISBNコードと呼ばれ、本屋やネット上で本を検索する際に役立っています。その13ケタの中に施されている数学的な工夫について紹介します... -

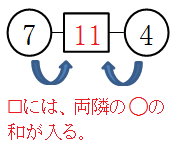
【数学的活動】パズルで始まり、方程式で理解!「数の鎖」で思考力を高めよう!
数学的な活動を取り入れたい先生方必見! 中1の方程式の単元で、数学が得意な生徒も苦手な生徒も楽しめる、パズル的な教材がこの「数の鎖」です。文字式や方程式の良さを感じられるだけでなく、思考力を要する課題にまで発展させられるため、様々なねらいや学力層に対応した教材となっています。 -

四次方程式の解の公式~フェラリが発見した経緯から公式を使った解き方まで~
ルドヴィコ・フェラーリが発見した4次方程式の解の公式とその証明、またその発見までの経緯について紹介します。